Категории и типы номеров
SNGL (single) — одноместный номер.
DBL (double) — двухместный номер с одной большой двуспальной кроватью.
TWIN (twin) — двухместный номер с двумя раздельными кроватями.
TRPL (triple) — трехместный номер.
4 PAX (quarter) — четырехместный номер.
5 ADL — пятиместный номер.
ЕХВ (extra bed) — дополнительная кровать.
Balcony Room — номер с балконом.
Connected Rooms — совмещенные номера, имеющие дверь-проход из одного в другой.
Duplex — двухэтажный номер.

Family Room — семейный номер, в который можно поселить от 4 человек, с большой площадью (часто из нескольких комнат).
Sitting area — зона для отдыха — часть номера, где располагаются кресла, журнальный столик, иногда также диван.
Standard — стандартная комната.
Studio — однокомнатный номер больше стандартного, как правило в апартаментах с небольшой кухней, совмещенной с комнатой.
Suite — номер повышенной комфортности, как правило — большая комната, имеющая зону для отдыха.
Mini Suite — номер улучшенной категории (лучше, чем Superior).
Junior Suite — номер повышенной комфортности: обычно большая комфортабельная комната с отгороженным спальным местом, преобразуемым днем в гостиную.
Senior Suite — номер повышенной комфортности, как правило двухкомнатный: гостиная и спальня.
Executive Suite — как правило, сьют с двумя спальнями.
King Suite — «королевский сьют», имеющий 2 спальни, гостиную и комнату для переговоров или рабочий кабинет.
Superior — комната большего размера, чем стандартная.
Honeymoon Room — номер для молодоженов, с большой кроватью KING SIZE и дополнительным презентом от отеля.
APT (appartment) — тип номеров, имеющих помимо зоны проживания, зону, оборудованную кухонным уголком, с набором посуды, электроплитой, чайником, как правило продаются без питания.
Типы номеров в отеле – InTur
Основные типы номеров в отелях, их описание и классификация.
Очень часто, выбирая тур в ту или иную страну, путешественники сталкиваются с разными аббревиатурами характеризующими тот или иной тип номера в отеле. Рассмотрим подробно расшифровку каждого типа номера в отдельности:
| Одноместный номер Single room – небольшие номера рассчитанные на одного человека. При бронировании в отеле номеров типа single room, обычно заселяют в стандартный двухместный номер.
|
|
| Стандартный номер Standard room
– стандартный однокомнатный типовой номер в отеле. В среднем размер номера Standard room составляет 10-20 квадратных метров
|
|
| Superior room – это улучшенная комната большего размера, чем стандартный типовой номер Standard room в отеле. В среднем размер номера Superior room составляет 20-25 квадратных метров.
|
|
Номер Deluxe room – это улучшенный во всех качествах тип номера большего размера, чем superior.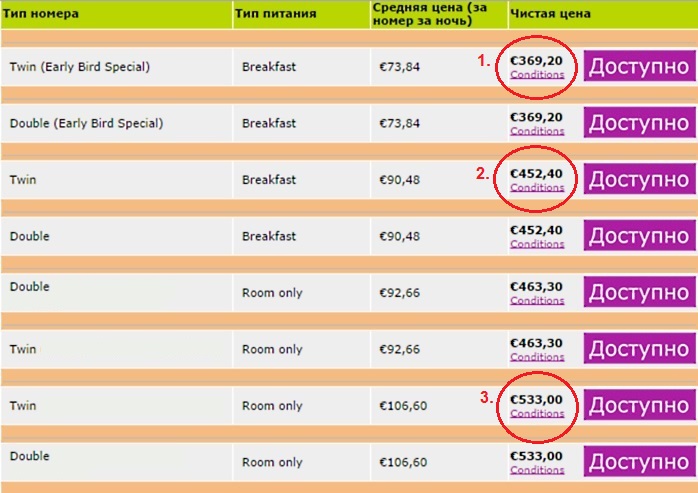 Размер номера Deluxe room начинается от 20 квадратных метров и может достигать 35-40 метров. Размер номера Deluxe room начинается от 20 квадратных метров и может достигать 35-40 метров.
|
|
| Номер Studio или Studio room – тип номера большего размера, чем номер Standard room. Это небольшие апартаменты с кухней, совмещенной с комнатой. Площадь – 20-25 кв. м и более
|
|
| Family suite и Family room |
|
| Junior suite – это самый простой тип номеров из категории suite, представляет собой однокомнатный номер повышенной комфортности и улучшенной планировки. В среднем размер номера 20-30 кв. м.
|
|
Сьюты Suite room это номер повышенной комфортности и улучшенной планировки, состоит не менее чем из двух комнат: отдельной спальни и зоны отдыха. Метраж, обычно, не меньше 40 кв.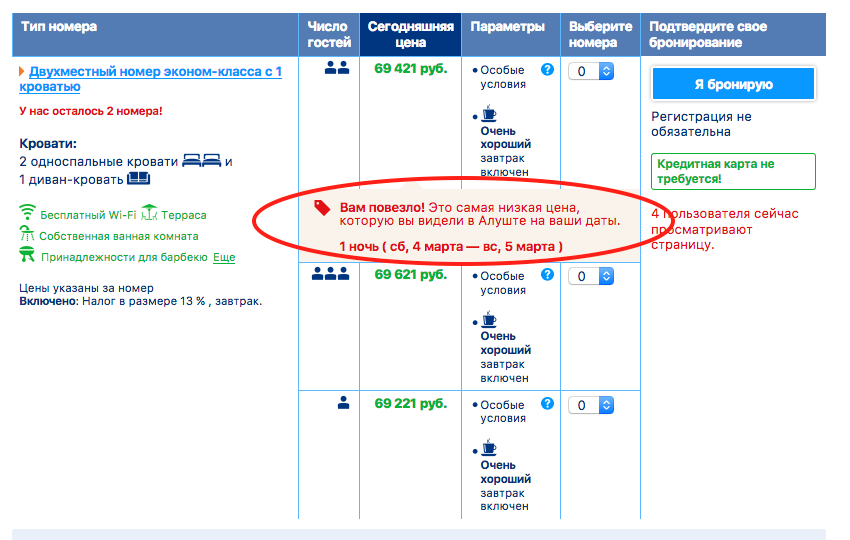 м. м.
|
|
| Executive Suite являются одними из самых роскошных номеров в отеле. Это номер с одной или двумя и более спальнями. Индивидуальное VIP-обслуживание и дополнительный сервис
|
|
| Номера Honeymoon Suite
для новобрачных идут отдельной категорией. Дизайн и обстановка номеров более романтическая, над интерьером работали профессиональные дизайнеры.
|
Подвиды типов номеров в отеле.
Double room («номер для двоих») – это двухместный тип номера с одной двуспальной кроватью, иногда, если площадь номера позволяет, можно поставить третью кровать. Дабл рум может иметь разновидности deluxe double room, studio double room, superior double room и пр.
Twin room («номер для двоих») двухместный номер с двумя раздельными кроватями, при необходимости может быть установлена третья кровать. Так же как и Double room, номера Twin room могут быть и deluxe double room, studio double room, superior double room и пр.
Connected Rooms («совмещенные комнаты») – это два соседних отдельных номера, между которыми есть запирающаяся дверь. Нередко используются для создания комнат типа “Family room”. Популярны для проживания семьи из нескольких человек.
Duplex («дуплекс») – двухуровневые номера. Достаточно большой тип номера, состоящий из двух, а иногда и более комнат, расположенных на двух этажах.
Apartment («квартира») – просторные номера с индивидуальной планировкой. Этот тип номера отчасти напоминают квартиру, нередко в апартаментах устанавливается кухня.
Business room («бизнес номер») – тип комнаты, предназначенный для работы и проживания деловых людей. Часто такие номера оснащены всем самым необходимым для работы – компьютером, принтером, факсом и т.п.
Типы и классификация видов из номера
Типы размещения DBL, SNGL, TRPL, CHD, EXB и др.
Типы питания в отелях – RO BB HB FB AI UAI и др.
Тип номера low cost room
Подписаться Рекламa на статье 0 0Во время выбора отеля путешественник может столкнуться с разными сокращениями и терминами. Например, main building, de lux и многими другими. Не всегда они понятны. А ведь очень важно правильно забронировать номер в отеле, чтобы в дальнейшем не возникло никаких проблем.
Например, main building, de lux и многими другими. Не всегда они понятны. А ведь очень важно правильно забронировать номер в отеле, чтобы в дальнейшем не возникло никаких проблем.
Разные аббревиатуры и сокращения могут застать врасплох новичков, которые впервые отправляются на отдых за границу.
Особенно часто людей интересует, тип номера low cost room — что это? Ответ будет приведён в статье.
Существуют разные типы номеров. Что значит low cost room? Нужно разобраться с основными видами, чтобы понять этот термин.
Каждый тип номера имеет свою стоимость и разные удобства. Существует недорогие номера и те, которые отличаются огромной стоимостью. Каждый человек может выбрать именно тот вариант, который подходит ему.
Существуют разные классификации гостиничных номеров. По размеру и составу номера делятся на:
- low cost room;
- standart room;
- suite;
- apartments;
- family room.
Также обозначения могут быть и другими. В представленной классификации самым маленьким номером является low cost room. Также в нем меньше всего удобств. Тогда как номера люкс и апартаменты являются наиболее дорогими, они имеют все необходимое для роскошного отдыха.
В представленной классификации самым маленьким номером является low cost room. Также в нем меньше всего удобств. Тогда как номера люкс и апартаменты являются наиболее дорогими, они имеют все необходимое для роскошного отдыха.
Для того чтобы понять, что означает такой тип номера и вообще сам термин, нужно обратиться к словарю. С его помощью можно точно понять значение любого термина.
Что такое low cost room? Перевод с английского говорит о том, что это недорогая комната. Само слово low cost означает «дешевый, недорогой, малозатратный».
Это словосочетание состоит из трех английских слов. Если заглянуть в словарь, то можно увидеть, что low означает «низкий, невысокий, тихий». Слово cost – это «стоимость, цена». Слово room в переводе на русский язык означает «комната».
Сам термин low cost можно увидеть в разных значениях. Часто его применяют, когда речь идёт о недорогих, бюджетных авиарейсах. Но если говорить об отельной сфере, где low cost room — тип номера, что это значит?
Если сложить все три слова вместе, то дословно их можно перевести как «низкая стоимость комнаты». То есть это наиболее выгодные предложения среди всех гостиничных номеров. Если сделать свободный перевод, то это словосочетание означает бюджетную комнату в отеле.
То есть это наиболее выгодные предложения среди всех гостиничных номеров. Если сделать свободный перевод, то это словосочетание означает бюджетную комнату в отеле.
Тип номера low cost room — что это? Это небольшие по размерам номера, но в которых есть все необходимые удобства. Например, душ и туалет, кровать и, возможно, телевизор.
В основном заказывают себе такой номер люди, которые хотят сэкономить средства. Они не могут себе позволить шикарные люкс апартаменты, поэтому останавливаются на этом варианте.
Чаще такие комнаты заказывают одинокие люди. Это могут быть студенты или молодые люди, которые имеют среднее материальное положение. Но заказать такую комнату может каждый желающий. Все чаще люди стараются как можно больше времени проводить именно на улице, а не в номере, поэтому для многих путешественников не является принципиальным размер их комнаты и её оснащение.
Преимущества и недостаткиКогда стало понятно, что это — тип номера low cost room, необходимо выяснить, стоит ли их заказывать.
Low cost room имеют свои плюсы и минусы. Конечно, основным преимуществом таких комнат является их небольшая стоимость. Благодаря этому позволить себе такое жилье на несколько суток может практически каждый желающий.
Также к плюсам этого типа номера можно отнести все необходимые удобства. В комнате будет кровать, тумбочка. Также может быть зеркало, телевизор или маленький холодильник.
Если говорить о недостатках, то стоит отметить, что в таких номерах нет расширенных удобств. Они просто обустроены. Также они небольшие по площади, поэтому такой вариант не будет удобным для нескольких людей или семей с детьми.
ВыводыПеред тем как забронировать гостиницу, нужно узнать про её месторасположение, типы номеров, которые здесь есть, а также удобства в выбранной комнате. Знание гостиничной терминологии значительно упростит выбор человека.
Что такое low cost room в отеле, теперь понятно. Каждый человек может решить, подходит ли для него такой вариант или нет. Для того чтобы понять это, человеку сначала нужно определиться с целью своей поездки. Если он хочет больше времени проводить в новом городе, а в номере появляться только по вечерам, то low cost room станет для него отличным вариантом.
Если он хочет больше времени проводить в новом городе, а в номере появляться только по вечерам, то low cost room станет для него отличным вариантом.
Кроме того, такие комнаты могут подойти для людей, которые планируют много путешествовать или, например, едут всего на один-два дня и не хотят тратить много денег на гостиницу.
Типы телефонных номеров в Службах коммуникации Azure — An Azure Communication Services concept document
- Чтение занимает 3 мин
В этой статье
Важно!
Доступность номера телефона сейчас ограничена платными подписками Azure, у которых есть адрес для выставления счетов в США и ресурсы Служб коммуникаций с расположением данных в США. Номера телефонов нельзя получить, имея пробные учетные записей или бесплатные кредиты Azure. Дополнительные сведения см. в разделе о допустимости подписки этого документа.
Номера телефонов нельзя получить, имея пробные учетные записей или бесплатные кредиты Azure. Дополнительные сведения см. в разделе о допустимости подписки этого документа.
Службы коммуникации Azure позволяют использовать номера телефонов для голосовых звонков и отправки SMS-сообщений через телефонную сеть общего пользования (ТСОП). В этом документе мы рассмотрим типы телефонных номеров, параметры коммуникации и доступность по регионам для планирования решения по обеспечению телефонной связи и отправки SMS с помощью Служб коммуникации.
Поддержка в подписках Azure
Чтобы получить номер телефона, требуется платная подписка Azure. Для пробных учетных записей и по бесплатным кредитам Azure невозможно получить номера телефонов.
Доступность номера телефона сейчас ограничена подписками Azure, у которых есть адрес для выставления счетов в США и ресурсы Служб коммуникаций с расположением данных в США.
Числовые типы и функции
Службы коммуникации предлагают два типа телефонных номеров: местные и бесплатные.
Местные номера
Местные (географические) номера — это 10-значные телефонные номера, состоящие из местных кодов городов в США. Например, +1 (206) XXX-XXXX — это местный номер с кодом города 206. Это телефонный код Сиэтла. Такие телефонные номера обычно используются физическими лицами и местными компаниями. Службы коммуникации Azure предлагают местные номера в США. Эти номера можно использовать для телефонных звонков, но они не подходят для отправки SMS.
Бесплатные номера
Бесплатные телефонные номера — это 10-значные телефонные номера с особыми телефонными кодами, на которые можно звонить бесплатно с любого номера телефона. Например, +1 (800) XXX-XXXX — это бесплатный номер в Северной Америке. Эти номера телефонов обычно используются для обслуживания клиентов. Службы коммуникации Azure предлагают бесплатные номера в США. Эти номера можно использовать для осуществления телефонных звонков и отправки SMS. Люди не могут использовать бесплатные номера сами.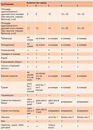 Их можно назначать только приложениям.
Их можно назначать только приложениям.
Выбор типа номера телефона
Если номер телефона будет использоваться приложением (например, для вызова или отправки сообщений от имени вашей службы), можете выбрать бесплатный или местный (географический) номер. Вы можете выбрать бесплатный номер, если приложение отправляет SMS-сообщения и (или) осуществляет вызовы.
Если номер телефона используется пользователем (например, пользователем вызывающего приложения), следует использовать местный (географический) номер телефона.
В следующей таблице перечислены все возможные типы номеров телефонов.
| Тип номера телефона | Пример | Доступность по странам | Возможности использования телефонного номера | Типичный сценарий использования |
|---|---|---|---|---|
| Местный (географический) | +1 (местный код города) XXX XX XX | США | Вызов (исходящий) | Назначение телефонных номеров пользователям в приложениях |
| Бесплатный номер | +1 (код, бесплатный в пределах региона) XXX XX XX | США | Вызов (исходящий), SMS (входящие или исходящие) | Назначение телефонных номеров системам интерактивного речевого ответа (ботам) и приложениям для работы с SMS |
Возможности телефонных номеров в Службах коммуникации Azure
Важно!
Службы коммуникации Azure не поддерживают вызовы экстренной помощи
Службы исходящих голосовых звонков в Службах коммуникации Azure нельзя использовать для вызова служб экстренной помощи. Для таких вызов используйте стандартную телефонную связь.
Для большинства телефонных номеров мы поддерживаем персонализированную настройку набора возможностей. Эти возможности можно выбрать при оформлении аренды телефонных номеров в Службах коммуникации Azure.
Доступные возможности зависят от страны, в которой вы работаете, варианта использования и выбранного типа телефонного номера. Эти возможности будут разными в зависимости от страны, так как это определяется нормативными требованиями. Службы коммуникации Azure предоставляют следующие возможности телефонных номеров:
- Только отправка SMS. Эта функция позволяет отправить пользователям SMS-сообщения. Такая функция может быть полезной для сценариев уведомления и двухфакторной проверки подлинности.
- Отправка и получение SMS. Эта функция позволяет отправлять сообщения пользователям и получать сообщения от них с помощью телефонных номеров. Она удобна для сценариев обслуживания клиентов.
- Только исходящие вызовы. Эта функция позволяет звонить пользователям и настраивать идентификатор вызывающей стороны для исходящих вызовов, выполняемых службой. Она удобна в сценариях обслуживания клиентов и голосовых уведомлений.
Доступность в различных регионах и странах
В следующей таблице показано, где можно получить телефонные номера различных типов, а также функции для входящих и исходящих вызовов и SMS, связанных с этими типами телефонных номеров.
| Тип номера | Место получения номера | Расположения вызываемого абонента | Прием вызовов от * | Расположения получателя сообщений | Расположения отправителя сообщений |
|---|---|---|---|---|---|
| Местный (географический) | США | США, Канада, Соединенное Королевство, Германия, Франция, США, +подробнее ** | США, Канада, Соединенное Королевство, Германия, Франция, США, +подробнее ** | Недоступно | Недоступно |
| Бесплатный номер | США | США | США | США | США |
* В настоящее время вы можете принимать вызовы только на номер Майкрософт, назначенный боту канала телефонии. * Дополнительные сведения о канале телефонии см. здесь. ** Дополнительные сведения о местах назначения и ценах для вызовов см. на странице цен.
Дальнейшие действия
Краткие руководства
Основная документация
Свой тип номер телефона
Например есть рабочий и есть мобильный. А у кого то есть стационарный и мобильный и все они рабочие. При этом другие стационарный и мобильный — могут быть — домашние.Или другой случай применения.
Как завести номера телефонов, чтобы было понятно, какой номер к какому отделу?
Телефон приемной: 78341111111
Телефон отдела кадров: 7834000000
Телефон отдела закупок: 78343333333
Если бы создать свой тип — отдел кадров.
——————————————————
Виталий
Добрый день. Можно ли как-то самому настраивать или добавлять названия телефонов: городской, мобильный, рабочий и т.п. Сейчас там несколько типов по умолчанию.
——————————————————
——————————————————
Консультации по Битрикс24
Добрый день, Виталий.
——————————————————
——————————————————
Консультации по Битрикс24
Вы можете добавить новый телефон нажав а кнопку Добавить. Будет несколько типов телефонов. Или Вы хотите создать свой тип?
http://joxi.ru/5mdgQJohvVo0lr
——————————————————
——————————————————
Виталий
Да, хочу свой тип. Это возможно?
——————————————————
——————————————————
Консультации по Битрикс24
Нет, к сожалению такой возможности не предусмотрено.
——————————————————
——————————————————
Виталий
Например есть рабочий и есть мобильный. А у кого то есть стационарный и мобильный и все они рабочие. При этом другие стационарный и мобильный — могут быть — домашние.
Или другой случай применения.
Как завести номера телефонов, чтобы было понятно, какой номер к какому отделу?
Телефон приемной: 78341111111
Телефон отдела кадров: 7834000000
Телефон отдела закупок: 78343333333
Если бы создать свой тип — отдел кадров. Или может вы в рамках компаний доработаете функционал отделов и подотделов у клиентов в CRM. Или как их завести в CRM правильно?
——————————————————
——————————————————
Консультации по Битрикс24
Я предлагаю Вам в карточке Компании созддать Дополнительное поле типа Строка, предположим, и туда записывать Телефоны.
——————————————————
— По пользовательским полям не происходит поиск из общего поиска, а тем более не происходит проверки на дубли. Так что лучше свой тип номера для начала
——————————————————
Консультации по Битрикс24
К сожалению, да, функционал для Ваших нужд не реализован.
Спасибо за обратную связь. У нас есть специальный портал, где мы собираем пожелания и голоса за них. Это помогает понять что наиболее востребовано — https://idea.1c-bitrix.ru/ Напишите пожалуйста предложение на портал идей. (Тогда если такая функция будет реализована, то вам придет уведомление с портала). Возможно оно там уже есть, тогда за него нужно будет просто проголосовать. Мы отслеживаем идеи и реализуем наиболее актуальные для пользователей.
——————————————————
——————————————————
Консультации по Битрикс24
Возможно, Вам смогут помочь наши партнеры. Настройку портала, адаптацию функционала под конкретные алгоритмы пользователя реализуют именно они. Здесь Вы сможете найти и выбрать того партнера, который находится в Вашем городе и чья ценовая политика Вас устроит. https://www.bitrix24.ru/partners
——————————————————
——————————————————
Консультации по Битрикс24
Виталий, я надеюсь, мой ответ Вам помог. Но если у Вас остались какие-то вопросы, не стесняйтесь их задавать — я и мои коллеги с радостью ответим на них. Хорошего вечера!
——————————————————
Ну да…
Тип номеров и Стоимость во Владимире
| Тип номера: | «Стандарт» |
|---|---|
| Спальных мест: | 2-3-4 (возможно доп место платно) |
| Площадь номера: | 25 кв.м. Комнат в номере: 1 Этаж: 2-3 |
| Санузел+Душ: | в номере (ванная) |
| Мебель: | односпальные или двуспальная кровати, диван-кровать, шкаф, стулья, прикроватные тумбочки, туалетный столик, зеркало |
| Удобства: |
сплит-система, телевизор, холодильник, посуда, балкон |
|
Цены на проживание: |
(за номер в сутки) |
| май | июнь | июль | август | сентябрь | октябрь | |
| 2-местный | 800 | 1500-1800 | 2000-2200 | 2200-1800 | 1600-1000 | 800 |
| 3-местный | 1200 | 1800-2200 | 2300-2500 | 2500-1800 | 1800-1300 | 1200 |
| 4-местный | 1500 | 2000-2500 | 2500-3000 | 2500-3000 | 2200-1600 | 1500 |
Указанные цены — ориентировочные, окончательную цену уточняйте при заказе.
| Тип номера: | «Люкс» |
|---|---|
| Спальных мест: | 2 (возможно доп место платно) |
| Площадь номера: | 40 кв.м. Комнат в номере: 2 Этаж: 2-3 |
| Санузел+Душ: | в номере (ванная) |
| Мебель: | двуспальная кровать, диван-кровать, кресло-кровать, шкаф, стулья, прикроватные тумбочки, туалетный столик, стол, зеркало |
| Удобства: |
сплит-система, телевизор, холодильник, посуда, балкон |
|
Цены на проживание: |
(за номер в сутки) |
| май | июнь | июль | август | сентябрь | октябрь |
| 1600 | 2500-3200 | 3200-4000 | 3200-4000 | 2500 | 1600 |
Указанные цены — ориентировочные, окончательную цену уточняйте при заказе.
Как изменить тип номеров, используемых в нумерованном списке в Word
По умолчанию Word использует арабские цифры (1, 2, 3 и т. Д.) При создании нумерованных списков. Однако вы можете изменить номера на другой тип или буквы. Символ после цифры или буквы также можно изменить.
ПРИМЕЧАНИЕ. Мы использовали Word 2016 для иллюстрации этой функции, но эта процедура работает и в 2013 году.
Выделите текст, который вы хотите преобразовать в нумерованный список. Нажмите стрелку вниз на кнопке «Нумерация» в разделе «Абзац» на вкладке «Главная». Некоторые форматы чисел доступны в разделе «Библиотека нумерации» в раскрывающемся меню, которое отображается. Если вы создали хотя бы один нумерованный список в текущем документе, числовые форматы, используемые в документе, отобразятся в разделе «Форматы номеров документов» раскрывающегося списка. Любые числовые форматы, использованные недавно в документе, перечислены в разделе «Недавно использованные форматы номеров». Вы можете выбрать любой из этих форматов для вашего текущего нумерованного списка. Если нужный формат отсутствует в раскрывающемся меню, выберите «Определить новый числовой формат».
В диалоговом окне «Определить новый числовой формат» выберите стиль в раскрывающемся списке «Числовой стиль».
Вы можете выбрать любой из следующих числовых и буквенных типов для использования в своих нумерованных списках.
- Арабский: 1, 2, 3, 4
- Прописные буквы: I, II, III, IV
- Строчный римский: I, II, III, IV
- Прописные буквы: A, B, C, D
- Строчные буквы: a, b, c, d
- Порядковые номера: 1, 2, 3, 4
- Номера слов: один, два, три, четыре
- Слово Ординалы: первый, второй, третий, четвертый
- Ведущие нули: 01, 02, 03, 04
В окне редактирования «Числовой формат» по умолчанию после цифры или буквы указывается точка. Если вы хотите изменить его на другой символ, такой как скобка («)», тире («-») или двоеточие («:»), удалите точку и введите нужный символ.
Раскрывающийся список «Выравнивание» позволяет указать, будет ли номер или буква выровнены по левому краю, по центру или справа в пространстве, выделенном для нумерации. По умолчанию выбрано «Слева». Выберите «По центру» или «Вправо», если вы хотите изменить выравнивание. Чтобы изменить шрифт цифр или букв в вашем списке, используйте кнопку «Шрифт». Когда вы закончите вносить изменения, нажмите «ОК». Нумерованный список создается аналогично примеру на изображении в начале этой статьи.
Если вы собираетесь настроить нумерацию в своем списке, возможно, вы захотите отключить автоматические нумерованные списки, чтобы Word автоматически не применял нумерацию по умолчанию при вводе ваших элементов.
Вы также можете легко пропустить нумерацию в нумерованных списках и создавать нумерованные списки с помощью клавиатуры в Word.
Типы чисел — различие и классификация
Можете ли вы представить, какой была бы ваша жизнь, если бы у вас не было возможности представить возраст, вес, дни рождения, время, результаты, банковские счета и номера телефонов? Десять математических цифр (от 0 до 9) используются для определения всех этих величин.
Числа — это цепочки цифр, используемые для представления количества. Величина числа указывает размер количества. Он может быть как большим, так и маленьким. Они существуют в разных формах, например, 3, 999, 0.351, 2/5 и т. Д.
Типы чисел в математике
Так же, как разные члены семьи живут в разных домах, разные числа принадлежат к одной семье, но имеют разные типы. Со временем различные комбинации десяти цифр были классифицированы на множество типов чисел. Эти шаблоны чисел отличаются друг от друга из-за разных представлений и свойств.
Натуральные числа
Натуральные числа или счетные числа — это самые основные типы чисел, которые вы впервые выучили в раннем детстве.Они начинаются с 1 и уходят в бесконечность, то есть 1, 2, 3, 4, 5, 6 и так далее. Их также называют положительными целыми числами. В установленной форме они могут быть записаны как:
{1, 2, 3, 4, 5,…}
Натуральные числа представлены символом N .
Целые числа
Целые числа — это набор натуральных чисел, включая ноль. Это означает, что они начинаются с 0 и увеличиваются до 1, 2, 3 и так далее, т.е.
{0, 1, 2, 3, 4, 5,…}
Целые числа представлены символом W .
Целые числа
Целые числа — это совокупность всех целых чисел и отрицательных чисел натуральных чисел. Они содержат все числа, лежащие между отрицательной бесконечностью и положительной бесконечностью. Они могут быть положительными, нулевыми или отрицательными, но не могут быть записаны в десятичной или дробной форме. Целые числа могут быть записаны в виде набора как
{…, -3, -2, -1, 0, 1, 2, 3,…}
Мы можем сказать, что все целые числа и натуральные числа являются целыми, но не все целые числа — это натуральные или целые числа.
Символ Z представляет целые числа.
Дроби
Дробь представляет собой части целого. Его можно записать в виде a / b , где a и b — целые числа, а b никогда не может быть равно 0. Все дроби являются рациональными числами, но не все рациональные числа являются дробями. .
Далее дроби сокращаются до правильных и неправильных дробей. Неправильные дроби — это дроби, в которых числитель больше знаменателя, в то время как для правильных функций верно обратное, т.е.е., знаменатель больше числителя. Примеры правильных дробей: 3/7 и 99/101, а 7/3 и 101/99 — неправильные дроби. Это означает, что неправильные дроби всегда больше 1.
Все завершающие десятичные дроби и повторяющиеся десятичные дроби могут быть записаны как дроби. Вы можете записать завершающую десятичную дробь 1,25 как 125/100 = 5/4. Повторяющееся десятичное число 0,3333 можно записать как 1/3.
Рациональные числа
Вы можете записывать рациональные числа в форме дробей. Слово «рациональный» происходит от слова «соотношение», поскольку рациональные числа — это отношения двух целых чисел.Например, 0,7 — рациональное число, потому что его можно записать как 7/10. Другими примерами рациональных чисел являются -1/3, 2/5, 99/100, 1,57 и т. Д.
Рассмотрим рациональное число p / q , где p и q — два целых числа. Здесь числитель p может быть любым целым числом (положительным или отрицательным), но знаменатель q никогда не может быть 0, поскольку дробь не определена. Кроме того, если q = 1, то дробь является целым числом.
Символ Q представляет рациональные числа.
Иррациональные числа
Иррациональные числа не могут быть записаны в дробной форме, т.е.они не могут быть записаны как отношение двух целых чисел. Вот несколько примеров иррациональных чисел: √2, √5, 0,353535…, π и так далее. Вы можете видеть, что цифры в иррациональных числах продолжаются до бесконечности без повторяющегося шаблона.
Символ Q обозначает иррациональные числа.
Действительные числа
Действительные числа — это совокупность всех рациональных и иррациональных чисел. Сюда входят все числа, которые можно записать в десятичной форме.Все целые числа являются действительными числами, но не все действительные числа являются целыми числами. Действительные числа включают в себя все целые числа, целые числа, дроби, повторяющиеся десятичные дроби, завершающие десятичные дроби и т. Д.
Символ R представляет действительные числа.
Мнимые числа
Числа, отличные от действительных, являются мнимыми или комплексными числами. Когда мы возводим в квадрат мнимое число, это дает отрицательный результат, что означает, что это квадратный корень из отрицательного числа, например, √-2 и √-5. Когда мы возводим эти числа в квадрат, получаем -2 и -5.Квадратный корень из отрицательной единицы представлен буквой i , т.е.
i = √-1
Пример 1
Что такое квадратный корень из -16? Запишите свой ответ, используя воображаемое число i .
Решение
- Шаг 1. Запишите форму квадратного корня.
√ (-16)
√ (16 × -1)
- Шаг 3. Разделите квадратные корни.
√ (16) × √ (-1)
- Шаг 4: Найдите квадратный корень.
4 × √ (-1)
- Шаг 5: Запишите в форме i.
4 i
Иногда вы получаете мнимое решение уравнений.
Пример 2
Решите уравнение,
x 2 + 2 = 0
Решение
- Шаг 1. Возьмите постоянный член с другой стороны уравнения.
x 2 = -2
- Шаг 2: извлеките квадратный корень с обеих сторон.
√ x 2 = + √-2 или -√-2
x = √ (2) × √ (-1)
x = + √2 i или -√2 i
- Шаг 4. Проверьте ответы, подставив значения в исходное уравнение, и посмотрите, получим ли мы 0.
x 2 + 2
(+ √2 i ) 2 + 2 = -2 + 2 = 0 (поскольку i = √-1 и квадрат i равен -1)
(-√2 i ) 2 + 2 = — 2 + 2 = 0 (поскольку i = √-1 и квадрат i равен -1)
То, что их имя «воображаемое» не означает, что они бесполезны.У них много приложений. Одно из самых больших применений мнимых чисел — их использование в электрических цепях. Вычисления силы тока и напряжения производятся в виде мнимых чисел. Эти числа также используются в сложных вычислительных вычислениях. В некоторых местах мнимое число также обозначается буквой j .
Комплексные числа
Мнимое число комбинируется с действительным числом, чтобы получить комплексное число. Он представлен как a + bi , где действительная часть и b являются комплексной частью комплексного числа.Действительные числа лежат на числовой прямой, а комплексные числа — на двумерной плоскости.
Как и мнимые числа, комплексные числа тоже не бесполезны. Они используются во многих приложениях, таких как «Сигналы и системы» и «Преобразование Фурье».
Простые числа и составные числа
Простые и составные числа противоположны друг другу. Простые числа — это целые числа без факторов, кроме них самих и 1, например 2, 3, 5, 7 и т. Д.Число 4 не является простым числом, потому что оно делится на 2. Аналогично, 12 также не является простым числом, потому что оно делится на 2, 3 и 4. Следовательно, 4 и 12 являются примерами составных чисел.
Трансцендентные числа
Числа, которые никогда не могут быть нулем (или корнем) полиномиального уравнения с рациональными коэффициентами, называются трансцендентными числами. Не все иррациональные числа являются трансцендентными числами, но все трансцендентные числа являются иррациональными числами.
Классификация чисел
Семейство чисел, которое мы видели выше, также можно разделить на разные категории. Это похоже на то, что в семье 20 человек, но они живут в двух совместных семейных домах по 10 человек в каждом, что означает, что 10 человек живут в одном доме. Мы можем сказать, что два или более типа чисел могут подпадать под одну категорию.
Дискретные и непрерывные числа
Типы счетных чисел называются дискретными числами, а типы чисел, которые не могут быть подсчитаны, называются непрерывными числами.Все натуральные, целые, целые и рациональные числа дискретны. Это потому, что каждый их набор является счетным. Набор действительных чисел слишком велик и не может быть посчитан, поэтому классифицируется как непрерывные числа. Если мы случайным образом возьмем два ближайших действительных числа, между ними все равно будет существовать бесконечно больше вещественных чисел; следовательно, их нельзя сосчитать.
Наборы номеров
Номера также можно классифицировать в виде наборов. Каждый тип числа является подмножеством другого типа числа.Например, натуральные числа — это подмножество целых чисел. Точно так же целые числа — это подмножество целых чисел. Набор рациональных чисел содержит все числа и дроби. Наборы рациональных чисел и иррациональных чисел образуют действительные числа. Действительные числа относятся к комплексным числам с мнимой частью как 0. Мы можем классифицировать эти числа в иерархической диаграмме, как показано ниже:
Натуральные числа могут быть далее сокращены до четных, нечетных, простых, простых, составных и точных квадратов. числа.
Предыдущий урок | Главная страница | Следующий урок
Какие бывают типы чисел? — Видео и стенограмма урока
Целые числа
Вернемся ко мне очень быстро, хотя я действительно живу в Купертино, Купертино является частью округа Санта-Клара. Это означает, что, поскольку я житель Купертино, я также житель округа Санта-Клара. Но обратное не обязательно верно, потому что не все, кто живет в округе Санта-Клара, живет в Купертино, поэтому вы должны быть осторожны, путешествуя туда и обратно.
Числа точно такие же. Если мы станем немного менее конкретными, то получим целые числа , . Все натуральные числа являются частью целых чисел, как и все люди, живущие в Купертино, также живут в округе Санта-Клара. Но есть одно целое число, которое не является натуральным числом. Это число 0. Итак, когда мы говорим о целых числах, мы говорим о числах, которые начинаются с 0 и начинают расти на 1, 2, 3 и так далее.
Целые числа
Если вернуться назад в моей ситуации, Купертино и округ Санта-Клара являются частями Калифорнии. Опять же, не все, кто живет в Калифорнии, живут в Санта-Кларе или, точнее, в Купертино. Но если вы живете в Купертино или Санта-Кларе, вы определенно живете в Калифорнии.
Делая шаг вперед в отношении чисел, мы получаем так называемые целые числа .Опять же, не все целые числа являются целыми числами и натуральными числами. Но все целые числа и натуральные числа являются целыми числами. Целые числа теперь также добавляют к отрицательным числам: -1, -2, -3 и так далее и далее в отрицательном направлении.
Rational Numbers
Сделав еще один шаг назад, я думаю, что большинство людей знают, что Калифорния — это штат, который является частью США, поэтому я также являюсь резидентом Соединенных Штатов. Опять же, каждый, кто является жителем Калифорнии, также является жителем США.С. Но не все, кто живет в США, живут в Калифорнии.
Эта тенденция продолжается с цифрами. Делая еще один шаг назад, мы приходим к так называемому рациональному числу . Новые пополнения в клубе — фракции. Это означает, что у нас могут быть такие вещи, как -1/2, 1/3, 3/4 или, может быть, 11/7.
Список становится немного сложнее писать, но, опять же, вы можете представить, что здесь много разных типов чисел. По-прежнему верно, что все предыдущие числа, которые мы упомянули, являются рациональными числами, но не все рациональные числа, особенно эти дроби, являются частью чисел в целых числах, целых числах или натуральных числах.
Иррациональные числа
Теперь, когда мы взяли место, где я живу, вплоть до того факта, что я живу в Америке, мы, вероятно, не должны упускать из виду людей, которые живут в разных странах. Но они в другой группе. Например, для людей, которые живут в Японии или Франции, вы не живете в Америке, поэтому вы являетесь частью отдельной группы.
То же самое происходит с числами. Есть отдельная группа чисел, которая не подходит к остальным. Их называют иррациональными числами . Иррациональные числа — это все числа, которые нельзя описать как дроби.
Таких разных номеров много. Одна из тех, о которых вы, возможно, слышали, называется «пи», то есть 3.14159 … и это все, что я знаю, но это продолжается вечно, и вы не можете представить число Пи с дробью, чтобы оно стало точным и правильным десятичным числом. Другой — квадратный корень из 2, что-то вроде 1,4, но опять же, десятичная дробь продолжается вечно, и нет дроби, которая могла бы ее представить.
Эти иррациональные числа представляют собой отдельную группу. Они не являются частью рациональных, натуральных или целых чисел; они не связаны, но разделены.
Реальные числа
Мне не нравится заканчивать рассказ о сепаратизме.Независимо от того, в какой стране вы живете, мы все жители планеты Земля. Цифры такие же. Они счастливы, и им нравится быть вместе. Все они живут под знаменем того, что называется действительными числами . Иррациональное и рациональное соединяются вместе, и вместе они образуют действительные числа.
Резюме урока
Напомним, что наиболее точным набором чисел являются натуральные числа: 1, 2, 3 и так далее, и так далее. Следующий шаг — это целые числа, и вы просто добавляете 0 к группе; все остальное остается прежним.Когда мы переходим к целым числам, мы складываем отрицательные числа: -3, -2, -1, 0, 1, 2, 3. Далее идут рациональные числа, а рациональные числа дают нам дроби.
Иррациональное является отдельным от этого, и это числа, которые не могут быть дробями, например пи и квадратный корень из 2. Действительные числа объединяют рациональное и иррациональное в один большой набор.
| Натуральные числа | Также известные как счетные числа, они включают 1,2,3,4,5,6… |
| Целые числа | Все натуральные числа, включая 0 |
| Целые числа | Все целые числа, включая отрицательные числа |
| Рациональные числа | Все целые числа, включая дроби |
| Иррациональные числа | Числа, которые нельзя выразить дробями, например, пи |
| Реальные числа | Все номера |
2.1 — Типы чисел
2.1 — Типы чисел2.1 — Типы чисел
Рассмотрим типы чисел. Посмотрим на натуральные и целые числа, целые числа, рациональные числа, иррациональные числа, действительные числа, мнимые числа и комплексные числа.Натуральные и целые числа
Начнем с натуральных чисел . Это числа 1, 2, 3,… (Символ… означает, что последовательность продолжается бесконечно.) Они используются для подсчета. Если мы включим ноль, то получим целых чисел , 0, 1, 2, 3,….
Натуральные и целые числа обычно считаются точными. (например, у машины 4 колеса, у паука 8 ног). Но иногда они приблизительны (например, в толпе было 1000 человек).
Вот целые числа, отображаемые в строке номера :
Целые числа
Теперь для каждого из чисел 1, 2, 3,… давайте создадим его напротив или отрицательное значение и поместим его напротив сторону числовой прямой, например:Мы говорим, что 1 и −1 — противоположности, 2 и −2 — противоположности и т. д.и мы также говорим, что −1 — противоположность 1, а 1 — противоположность −1.
Отрицательные числа используются для описания долгов, а не активов, температуры ниже нуля в отличие от температур выше нуля, высоты ниже уровня моря, а не высоты над уровнем моря и т. д.
Набор чисел…, −3, −2, −1, 0, 1, 2, 3,… (целые числа и их противоположности) называется целыми числами .
Рациональные числа
Далее идут рациональные числа.Они являются обобщением общие дроби, поэтому давайте сначала рассмотрим их. Помните, что дробное обозначение a / b означает, что мы разбиваем что-то на b равных частей, и у нас есть a таких частей. Например, если мы разбиваем пирог на 4 части, и у нас есть 1 кусок, то у нас есть 1/4 части пирога:Рациональное число определяется как любое число, которое может быть выражено как частное или отношение из два целых числа .Мы используем то же обозначение дробей для выражения рациональных чисел:
Целое число a называется числителем, а целое число b — знаменателем. Знаменатель не может быть равен нулю.
Обратите внимание, что если a и b являются натуральными числами (1, 2, 3 и т. Д.), То мы получаем обычную дробь. Таким образом, рациональные числа включают обыкновенные дроби.
Обратите внимание, что 3/1 = 3 и −5/1 = −5, поэтому рациональные числа включают все целые числа.
Рациональные числа также можно записывать в десятичной системе счисления вместо дробной. Например:
1/4 = 0,25Десятичная запись 0,25 означает буквально «25/100», а 25/100 и 1/4 — эквивалентные дроби.
Обратите внимание, что некоторые рациональные числа не имеют точного десятичного эквивалента. Например 1/3 примерно равно 33/100, но не совсем:
1/3 ≈ 0,33(Символ ≈ означает « примерно равно ».) Рациональными числами обычно считаются , точные . По этой причине программа Algebra Coach не преобразует дроби в десятичные, когда работает в точном режиме.
Иррациональные числа
Иррациональные числа — это числа, которые нельзя выразить как отношение двух целых чисел. Примерами являются, а также квадратные корни из многих других чисел, и специальные числа, такие как e и π. Получается, что иррациональных чисел столько же как рационально.У иррациональных чисел нет точных десятичных эквивалентов. Чтобы написать любое иррациональное число в десятичной системе счисления потребуется бесконечное количество десятичных цифр. Таким образом, это только приблизительные значения:≈ 1,732, e ≈ 2,718 и π ≈ 3,14,По этой причине программа Algebra Coach не преобразует иррациональные числа в десятичные. когда он работает в точном режиме.
Реальные числа
Рациональные числа и иррациональные числа вместе составляют действительных чисел .Реальные числа Говорят, что это плотный . Они включают в себя все числа в числовой строке.Числовая строка полезна для понимания порядка чисел . Меньшие числа левее а большие числа — правее.
Мы используем символ <для обозначения « меньше » и символ> означает « больше ». Вот несколько примеров использования этих символов:
- 5 <8, потому что 5 находится слева от 8.
- −5 <2, потому что −5 находится слева от 2. Фактически любое отрицательное число меньше любого положительного числа.
- 5 <8 и 8> 5 — два способа констатировать один и тот же факт.
- 3,14 <π <3,15 Я называю это «меньше, чем бутерброд». Это означает, что 3.14 <π, а также π <3.15. Другими словами, число π находится где-то между 3,14 и 3,15.
Щелкните здесь, чтобы получить дополнительную информацию о точности и значащих числах.
Мнимые числа и комплексные числа
Если действительные числа включают каждое число в числовой строке, то какие еще могут быть числа? Чтобы ответить на этот вопрос, подумайте, как мы до сих пор строили систему счисления:- Мы начали с целых чисел (например, 3)
- Нам нужны были противоположности для этих чисел, поэтому мы создали целые числа (числа вроде −3)
- Мы хотели разделить эти числа, но нуждались в рациональных числах для описания некоторые результаты (числа вроде 3/4)
- Мы хотели извлечь квадратный корень из этих чисел, но нам потребовались иррациональные числа, чтобы описать некоторые результаты (например,грамм. )
Где на числовой прямой идут мнимые и комплексные числа? Ответ — нет. На этом рисунке показана комплексная плоскость . Он содержит числовую строку (которая теперь называется действительной осью ) и новой осью, называемой мнимая ось , перпендикулярная ей. Реальные числа лежат на действительной оси, мнимые числа лежат на мнимой оси, а комплексные числа обычно лежат вне действительной оси, либо над ним, либо под ним.
Программа Algebra Coach может работать в реальном или сложном режиме. В реальном режиме не будет выполнить любую операцию, которая приводит к не действительному числу (например, извлечение квадратного корня отрицательного числа).
Щелкните здесь, чтобы получить дополнительную информацию о комплексных числах.
Если вы нашли эту страницу в поиске в Интернете, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
натуральных, целых, рациональных, иррациональных, действительных чисел и выше
Натуральные числа
натуральное число (или , считая ) числа — это 1,2,3,4,5 и т. Д. много натуральных чисел. Набор натуральных чисел, {1,2,3,4,5, …}, иногда для краткости пишется N .
Целые числа — натуральные числа вместе с 0.
(Примечание: некоторые учебники не согласны с этим и говорят, что натуральные числа включают 0.)
Сумма любые два натуральных числа также являются натуральными числами (например, 4 + 2000 = 2004), а произведение любых двух натуральных чисел натуральное число (4 × 2000 = 8000). Этот однако это неверно для вычитания и деления.
Целые числа
Целые числа — это набор действительных чисел, состоящий из натуральных чисел, их обратных аддитивных чисел и нуля.
{…, — 5, −4, −3, −2, −1,0,1,2,3,4,5, …}
Набор целых чисел иногда написано J или Z для краткости.
сумма, произведение и разность любых двух целых чисел также являются целыми числами. Но это не относится к делению … просто попробуйте 1 ÷ 2.
Рациональные числа
Рациональные числа те числа, которые можно выразить как отношение между два целых числа. Например, дроби 13 и −11118 являются рациональное число. Все числа входят в рациональные числа, поскольку любое целое число z можно записать как отношение z1.
Все десятичные дроби, которые заканчиваются, являются рациональными числами (начиная с 8.27 можно записать как 827100.) Десятичные дроби которые после некоторой точки имеют повторяющийся узор, также являются рациональными: например,
0,0833333 …. = 112.
Множество рациональных чисел замкнуто относительно всех четырех основных операций, то есть для любых двух рациональных чисел их сумма, разница, произведение и частное также являются рациональным числом (пока мы не делим на 0).
Иррациональные числа
Иррациональное число — это число, которое нельзя записать в виде отношения (или дроби).В десятичной форме он никогда не заканчивается и не повторяется. В древние греки обнаружили, что не все числа рациональны; там — это уравнения, которые нельзя решить с помощью отношений целых чисел.
Первое такое уравнение для изучения было 2 = x2. Какие само число умноженное на 2?
2 является около 1,414, поскольку 1,4142 = 1,999396, что близко к 2. Но вы никогда не попадете точно, возведя дробь в квадрат (или завершив десятичный). Квадратный корень из 2 — иррациональное число, то есть его десятичный эквивалент продолжается вечно, без повторяющегося образца:
2 = 1.41421356237309 …
Другой известный иррациональный числа золотое сечение , число с большим значение для биологии:
1 + 52 = 1,61803398874989 …
π (пи), отношение длины окружности к ее диаметру:
π = 3,14159265358979 …
и е, самое важное число в исчислении:
е = 2,71828182845904 …
Иррациональные числа могут быть далее подразделены на алгебраических чисел , которые являются решениями некоторого полиномиального уравнения (например, 2 и золотое сечение), и трансцендентных чисел , которые не являются решениями какого-либо полиномиального уравнения.π и e оба трансцендентны.
Реальные числа
Действительные числа — это набор чисел, содержащий все рациональные числа и все иррациональные числа. Настоящие числа — это «все числа» в числовой строке. Существует бесконечно много действительных чисел, как и бесконечно много чисел в каждом из других наборов чисел. Но можно доказать, что бесконечность действительных чисел на больше бесконечности.
«Меньше», или счетных бесконечности целых чисел и rationals иногда называют ℵ0 (alef-naught), и бесчисленное множество бесконечности реалов называется ℵ1 (алеф-он).
Есть еще «большие» бесконечности, но для этого вам следует взять курс теории множеств!
Комплексные числа
Комплексные числа — множество {a + bi | a и b — действительные числа}, где i — мнимая единица, −1. (нажмите здесь, чтобы подробнее о мнимых числах и операциях с комплексными числами).
Комплексные числа включают набор действительных чисел. Действительные числа в сложной системе записываются в виде a + 0i = a. реальное число.
Этот набор иногда бывает записывается как C для краткости.Набор комплексных чисел важно, потому что для любого полинома p (x) с коэффициентами действительного числа все решения p (x) = 0 будут в C .
За пределами …
Есть и «большие» наборы чисел, используемых математиками. Кватернионы , открытые Уильямом Х. Гамильтоном в 1845 году, образуют систему счисления с тремя разные мнимые единицы!
— HTML: язык разметки гипертекста
элементы типа число используются, чтобы позволить пользователю ввести число.Они включают встроенную проверку для отклонения нечисловых записей.
Браузер может выбрать отображение шаговых стрелок, позволяющих пользователю увеличивать и уменьшать значение с помощью мыши или касания пальцем.
В браузерах, которые не поддерживают ввод типа число , ввод числа число возвращается к типу текст .
A Число , представляющее значение числа, введенного во входные данные. Вы можете установить значение по умолчанию для ввода, включив число в атрибут значение , например:
Помимо атрибутов, обычно поддерживаемых всеми типами , эти атрибуты поддерживают входы типа номер .
список
Значения атрибута списка — это id элемента , расположенного в том же документе. предоставляет список предопределенных значений, которые можно предложить пользователю для этого ввода. Любые значения в списке, несовместимые с типом , не включаются в предлагаемые параметры. Предоставленные значения являются предложениями, а не требованиями: пользователи могут выбрать из этого предопределенного списка или указать другое значение.
макс.
Максимальное значение для этого входа. Если значение , введенное в элемент, превышает это значение, элемент не проходит проверку ограничения. Если значение атрибута max не является числом, то у элемента нет максимального значения.
Это значение должно быть больше или равно значению атрибута min .
мин.
Минимальное значение для этого ввода. Если значение элемента меньше этого, элемент не проходит проверку ограничения.Если для мин. указано значение, которое не является допустимым числом, вход не имеет минимального значения.
Это значение должно быть меньше или равно значению атрибута max .
заполнитель Атрибут заполнитель — это строка, которая дает пользователю краткую подсказку относительно того, какая информация ожидается в поле. Это должно быть слово или короткая фраза, демонстрирующая ожидаемый тип данных, а не пояснительное сообщение.Текст не должен содержать символов возврата каретки или перевода строки.
Если содержимое элемента управления имеет одну направленность (LTR или RTL), но должно представлять заполнитель с противоположной направленностью, вы можете использовать символы форматирования двунаправленного алгоритма Unicode, чтобы переопределить направленность внутри заполнителя; см. Переопределение двунаправленного текста с помощью управляющих символов Unicode в Алгоритме двунаправленного текста Unicode для этих символов.
только для чтения
Логический атрибут, который, если он присутствует, означает, что это поле не может редактироваться пользователем.Однако его значение все еще можно изменить с помощью кода JavaScript, напрямую установив свойство HTMLInputElement value .
Примечание: Поскольку поле только для чтения не может иметь значение, требуется не оказывает никакого влияния на входные данные с указанным атрибутом только для чтения .
step
Атрибут step — это число, которое указывает степень детализации, которой должно придерживаться значение, или специальное значение - любое значение , что описано ниже.Действительны только значения, которые равны основанию для пошагового выполнения ( мин. , если указано, значение, в противном случае и соответствующее значение по умолчанию, если ни одно из них не предусмотрено).
Строковое значение любое означает, что пошаговое выполнение не подразумевается, и разрешено любое значение (за исключением других ограничений, таких как мин. и макс. ).
Примечание: Когда данные, введенные пользователем, не соответствуют пошаговой конфигурации, пользовательский агент может округлить до ближайшего допустимого значения, предпочитая числа в положительном направлении, когда есть два одинаково близких варианта.
Значение шага по умолчанию для входов число — 1 , что позволяет вводить только целые числа — , если база шага не является целым числом.
элементов могут помочь упростить вашу работу при создании пользовательского интерфейса и логики для ввода чисел в форму. Когда вы создаете числовой ввод с правильным значением типа , числом , вы получаете автоматическую проверку того, что введенный текст является числом, и обычно набором кнопок вверх и вниз для пошагового перехода значения вверх и вниз.
Предупреждение: По логике, вы не должны иметь возможность вводить символы внутри числового ввода, кроме цифр. Похоже, среди браузеров есть некоторые разногласия по этому поводу; см. ошибку 1398528.
Примечание: Пользователь может повозиться с вашим HTML за кулисами, поэтому ваш сайт не должен использовать простую проверку на стороне клиента для каких-либо целей безопасности. Вы должны проверить на стороне сервера любую транзакцию, в которой предоставленное значение может иметь последствия для безопасности любого рода.
Мобильные браузеры еще больше улучшают взаимодействие с пользователем, показывая специальную клавиатуру, более подходящую для ввода чисел, когда пользователь пытается ввести значение.
Простой ввод числа
В самом простом виде ввод числа может быть реализован следующим образом:
Введенное число считается действительным, если оно пусто и когда введено одно число, но в остальном недействительно.Если используется требуемый атрибут , входные данные больше не считаются действительными, если они пусты.
Заполнители
Иногда бывает полезно предложить контекстную подсказку относительно того, какую форму должны принимать входные данные. Это может быть особенно важно, если в дизайне страницы нет описательных меток для каждого . Здесь на помощь приходят заполнители . Заполнитель — это значение, наиболее часто используемое для подсказки относительно формата, в котором ввод должен принимать значение , значение .Он отображается внутри поля редактирования, когда значение элемента равно "" . После ввода данных в поле заполнитель исчезает; если поле пусто, заполнитель появляется снова.
Здесь у нас есть входное число , число с заполнителем «, кратное 10, ». Обратите внимание, как заполнитель исчезает и появляется снова, когда вы манипулируете содержимым поля редактирования.
Управление размером шага
По умолчанию кнопки «вверх» и «вниз», позволяющие перемещать число вверх и вниз, будут увеличивать или уменьшать значение на 1.Вы можете изменить это, предоставив атрибут step , который принимает в качестве своего значения число, определяющее величину шага. В нашем примере выше есть заполнитель, в котором говорится, что значение должно быть кратно 10, поэтому имеет смысл добавить значение шага , равное 10 :
В этом примере вы должны обнаружить, что стрелки шага вверх и вниз будут увеличивать и уменьшать значение каждый раз на 10, а не на 1.Вы по-прежнему можете вручную ввести число, не кратное 10, но оно будет считаться недействительным.
Указание минимального и максимального значений
Вы можете использовать атрибуты min и max , чтобы указать минимальное и максимальное значение, которое может иметь поле. Например, давайте дадим нашему примеру минимум 0 и максимум 100 :
В этой обновленной версии вы должны обнаружить, что кнопки шага вверх и вниз не позволят вам опускаться ниже 0 или выше 100.Вы по-прежнему можете вручную ввести число за пределами этих границ, но оно будет считаться недействительным.
Разрешение десятичных значений
Одна проблема с числовым вводом заключается в том, что размер шага по умолчанию равен 1. Если вы попытаетесь ввести число с десятичной дробью (например, «1.0»), оно будет считаться недействительным. Если вы хотите ввести значение, требующее десятичных знаков, вам необходимо отразить это в значении шага (например, шаг = "0,01" , чтобы разрешить десятичные дроби до двух знаков после запятой). Вот простой пример:
Обратите внимание, что в этом примере допускается любое значение от 0,0 до 10,0 с десятичными знаками до двух разрядов. Например, «9,52» допустимо, а «9,521» - нет.
Управление размером ввода
элементы типа число не поддерживают атрибуты изменения размера формы, такие как размер . Вам придется прибегнуть к CSS, чтобы изменить размер этих элементов управления.
Например, чтобы настроить ширину поля ввода так, чтобы она была настолько широкой, насколько это необходимо для ввода трехзначного числа, мы можем изменить наш HTML, включив в него идентификатор и , и сократить наш заполнитель, поскольку поле будет слишком узким. для текста, который мы использовали до сих пор:
Затем мы добавляем CSS, чтобы сузить ширину элемента с помощью селектора id #number :
Результат выглядит следующим образом:
Предлагаемые значения
Вы можете предоставить список параметров по умолчанию, из которых пользователь может выбрать, указав атрибут list , который содержит в качестве своего значения id из , который, в свою очередь, содержит один элемент для каждого предлагаемого значения.Значение каждого параметра является соответствующим предлагаемым значением для поля ввода числа. опции
Мы уже упоминали ряд функций валидации входов number , но давайте рассмотрим их сейчас:
-
required). - Чтобы сделать пустую запись недействительной, можно использовать обязательный атрибут
- Вы можете использовать атрибут
step, чтобы ограничить допустимые значения определенным набором шагов (например, кратными 10). - Вы можете использовать атрибуты
мин.имакс., чтобы ограничить допустимые значения нижними и верхними границами.
В следующем примере демонстрируются все вышеперечисленные функции, а также используется некоторый CSS для отображения действительных и недопустимых значков, в зависимости от значения input :
<форма>
Требуется
Попробуйте отправить форму с другими введенными недопустимыми значениями - e.г., без значения; значение ниже 0 или выше 100; значение, не кратное 10; или нечисловое значение - и посмотрите, как сообщения об ошибках, которые выдает вам браузер, отличаются от других.
CSS, примененный к этому примеру, выглядит следующим образом:
div {
нижнее поле: 10 пикселей;
}
input: invalid + span: after {
содержание: '✖';
отступ слева: 5 пикселей;
}
input: valid + span: after {
содержание: '✓';
отступ слева: 5 пикселей;
}
Здесь мы используем псевдоклассы : invalid и : valid для отображения соответствующего недопустимого или допустимого значка в качестве сгенерированного содержимого на соседнем элементе в качестве визуального индикатора достоверности.
Мы разместили его на отдельном элементе для дополнительной гибкости. Некоторые браузеры не очень эффективно отображают сгенерированный контент для некоторых типов входных данных формы. (Прочтите, например, раздел о проверке .)
Предупреждение: HTML-форма валидации - это , а не , заменяющая серверные сценарии, которые гарантируют, что введенные данные находятся в правильном формате!
Для кого-то слишком легко внести изменения в HTML, которые позволят им обойти проверку или полностью удалить ее.Также есть возможность обойти ваш HTML и отправить данные прямо на ваш сервер.
Если ваш серверный код не может проверить данные, которые он получает, может случиться катастрофа, когда отправляются неправильно отформатированные данные (или данные слишком большого размера, неправильного типа и т. Д.).
Проверка шаблона
Элементы не поддерживают использование атрибута шаблона для приведения введенных значений в соответствие с определенным шаблоном регулярного выражения.
Обоснование этого состоит в том, что числовые входы не будут действительными, если они содержат что-либо, кроме чисел, и вы можете ограничить минимальное и максимальное количество действительных цифр, используя атрибуты min и max (как описано выше).
Мы уже рассмотрели тот факт, что по умолчанию приращение составляет 1 , и вы можете использовать атрибут step , чтобы разрешить десятичный ввод. Давайте рассмотрим подробнее.
В следующем примере представлена форма для ввода роста пользователя.По умолчанию принимается высота в метрах, но вы можете нажать соответствующую кнопку, чтобы изменить форму, чтобы вместо этого принимать футы и дюймы. Высота в метрах вводится с двумя десятичными знаками.
HTML-код выглядит так:
<форма>
Введите свой рост -
Вы увидите, что мы используем многие из атрибутов, которые уже рассматривали в статье ранее.Поскольку мы хотим принять значение метра в сантиметрах, мы установили значение шага равным 0,01 , чтобы такие значения, как 1,78 , не считались недопустимыми. Мы также предоставили заполнитель для этого ввода.
Изначально мы скрыли вводы футов и дюймов, используя style = "display: none;" , так что метры являются типом записи по умолчанию.
Теперь о CSS. Это очень похоже на стиль проверки, который мы видели раньше; здесь ничего примечательного.
div {
нижнее поле: 10 пикселей;
положение: относительное;
}
input [type = "number"] {
ширина: 100 пикселей;
}
input + span {
отступ справа: 30 пикселей;
}
input: invalid + span: after {
позиция: абсолютная;
содержание: '✖';
отступ слева: 5 пикселей;
}
input: valid + span: after {
позиция: абсолютная;
содержание: '✓';
отступ слева: 5 пикселей;
}
И, наконец, JavaScript:
пусть meterInputGroup = document.querySelector ('. MeterInputGroup');
пусть feetInputGroup = документ.querySelector ('. feetInputGroup');
let meterInput = document.querySelector ('# метров');
let feetInput = document.querySelector ('# футов');
let дюймыInput = document.querySelector ('# дюймов');
пусть switchBtn = document.querySelector ('input [type = "button"]');
switchBtn.addEventListener ('щелчок', function () {
if (switchBtn.getAttribute ('class') === 'meter') {
switchBtn.setAttribute ('класс', 'ноги');
switchBtn.value = 'Введите высоту в метрах';
meterInputGroup.style.display = 'нет';
feetInputGroup.style.display = 'блок';
feetInput.setAttribute ('обязательно', '');
дюймыInput.setAttribute ('обязательно', '');
meterInput.removeAttribute («обязательно»);
meterInput.value = '';
} еще {
switchBtn.setAttribute ('класс', 'метры');
switchBtn.value = 'Введите высоту в футах и дюймах';
meterInputGroup.style.display = 'блок';
feetInputGroup.style.display = 'нет';
feetInput.removeAttribute ('обязательно');
дюймыInput.removeAttribute ('обязательно');
meterInput.setAttribute ('обязательно', '');
футовВход.значение = '';
дюймыInput.value = '';
}
});
После объявления нескольких переменных к кнопке добавляется прослушиватель событий для управления механизмом переключения. Это довольно просто, в основном это связано с изменением класса кнопки и и обновлением отображаемых значений двух наборов входов при нажатии кнопки.
(Обратите внимание, что здесь мы не конвертируем метры и футы / дюймы туда и обратно, что, вероятно, могло бы сделать реальное веб-приложение.)
Примечание: Когда пользователь нажимает кнопку, требуемый атрибут (-ы) удаляется из входных данных, которые мы скрываем, и очищаем значение атрибута (-ов) . Это сделано для того, чтобы форму можно было отправить, если оба набора входных данных не заполнены. Это также гарантирует, что форма не будет отправлять данные, которые пользователь не имел в виду.
Если вы этого не сделали, вам придется заполнить и метра в футах / дюймах, чтобы отправить форму!
таблицы BCD загружаются только в браузер
различных видов чисел - пузырьковые простые числа
Числа - это умственные инструменты
Иногда мы думаем, что числа - это просто числа, но на самом деле их много.Числа - это инструменты ума. Нам нужны разные инструменты для решения разного рода проблем. Это приводит нас к…
Пицца часто упоминается в разговорах о дробях. Извините, что меняю тему, но это действительно брюссельская капуста ?! Да! Они обжарены до хрустящей корочки на оливковом масле и чесноке, и они потрясающие. Мы находимся в Калифорнии, где очень ценятся эксперименты с полезными ингредиентами и ароматизаторами. Кроме того, чего вы ждете от создателей обучающих игр? Наша философия - искать способы превратить полезные для нас продукты в вкусные угощения!Подсчет чисел
Когда вы считаете ночью воображаемых овец, чтобы они заснули, вы начинаете с одной, переходите к двум и так далее.У вас никогда не бывает нулевой овцы, потому что вы начинаете считать, когда представляете первую. Для подсчета таких вещей, как овцы, используется счетное число .
Натуральные числа
Хотя число ноль кажется нам очевидным понятием, это, по-видимому, результат нашего современного воспитания. Конечно, древние люди были хорошо знакомы с отсутствием чего-либо, но с точки зрения счетного числа, если у вас чего-то нет, вы не можете это сосчитать, поэтому вы не можете описать это числом.Прошло много времени, прежде чем мы начали думать, что иметь реальное число - это нормально, когда мы ничего не имеем.
Хотя идеи, связанные с нулем, возникали в разных местах и в разные времена, математиком, первым определившим ноль в современном математическом смысле, был Брахмагупта в своей книге Brahmasphutasiddhanta , написанной в 628 году, когда ему было 30 лет. В нем также описаны правила арифметики с отрицательными числами, и, что удивительно для меня, он был полностью написан в стихах! Что бы вы подумали, если бы ваша следующая книга по математике была полностью посвящена стихам? В настоящее время, когда мы включаем число ноль в счетные числа, мы называем это натуральными числами .
Целые числа
Трудно представить, какой была бы отрицательная овца. Однако отрицательные числа действительно полезны для некоторых вещей.
Например, предположим, что я репетитор по математике (как вы уже догадались, я действительно им учусь). Обычно мои ученики платят мне перед репетиторством, иногда за целый месяц сразу, иногда только за одно занятие и так далее. Я слежу за тем, сколько денег они мне дали и сколько я списал с них, чтобы убедиться, что они не переплачивают или недоплачивают мне.Иногда кто-то забывает чек, но я все равно их обучаю. Поскольку они теперь должны мне деньги, я просто записываю это как отрицательное число в их аккаунте, и когда они наконец платят мне, я добавляю положительное число к отрицательному, и их счет (обычно) снова становится положительным. Поскольку все эти числа являются целыми числами, но иногда положительными, а иногда отрицательными, это целых чисел .
Все натуральные числа являются целыми числами, но целые отрицательные числа также являются целыми числами.
Что это за число -1? или -4? или -9?
Это целые числа.
Целые числа
Математики обычно соглашаются с определениями подсчета чисел, натуральных и целых чисел. Однако они не совсем соответствуют термину целые числа. Целые числа как бы подчеркивают тот факт, что дроби недопустимы, не вдаваясь в подробности вопроса о том, разрешены ли отрицательные числа или ноль. Поскольку, говоря о простых и составных числах, мы неоднократно подчеркивали, что простые числа и составные числа должны быть больше единицы, ноль и отрицательные числа не являются проблемой.Этот веб-сайт в основном ориентирован на простые числа, поэтому мы решили использовать целых чисел в большинстве случаев, потому что это наиболее понятный вариант.
Рациональные числа
Рациональные числа обозначают дробные части. Почти на каждом уроке о рациональных числах будет пицца! Во-первых, большинству людей действительно нравится пицца, и это повод поговорить об этом. Но также большинство пицц слишком велики, чтобы один человек мог их съесть самостоятельно, и мы разрезали их на кусочки.В отличие от некоторых продуктов, которые нарезают ложкой на порции или нарезают на блоки, когда вы смотрите на кусок пиццы, обычно легко определить, на сколько ломтиков была нарезана вся пицца. Когда вы говорите о том, чтобы разбить вещи на равные части, а затем сгруппировать эти части, вы попали в мир дробей. Рациональные числа - это просто формальное математическое слово, обозначающее числа с дробями.
Иррациональные числа
Оказывается, есть способы разбить числа, которые невозможно сделать, разбив их на равные части, а затем сгруппировав эти части вместе (какими бы незаметно крошечными ни были крошки).В это трудно поверить, но есть такие довольно важные и распространенные числа, которые называются иррациональными числами . Математики любят доказывать невероятные вещи, и некоторые доказательства иррациональности чисел действительно умны. Докажу ли я, что какое-то важное число (например, пи или квадратный корень из 2) не является рациональным числом? Я не хочу слишком отвлекаться, делая это здесь, но если вы один из тех, кто хотел, чтобы я это сделал, я думаю, что вы математик!
Действительные числа
Иррациональные числа сами по себе не так полезны для решения общих задач, как другие виды чисел, о которых мы говорили.До сих пор каждая группа чисел, о которой мы говорили, включает предыдущую. Например, натуральные числа включают счетные числа, целые числа включают натуральные числа, а рациональные числа включают целые числа. Но иррациональные числа не включают рациональные числа. В частности, в иррациональных числах отсутствуют некоторые элементы, необходимые для большинства видов работы, например, числа ноль и единица.
С иррациональными числами можно справиться двумя способами.Один из них - доказать, что то или иное число иррационально. Другой - объединить рациональные и иррациональные числа вместе, чтобы создать действительных чисел .
Вот еще кое-что интересное о реальных числах. Они не только являются комбинацией рациональных и иррациональных чисел, но они также представляют собой комбинацию алгебраических чисел и трансцендентных чисел . Мы не будем вдаваться в подробности, что такое алгебраические и трансцендентные числа (это требует подробного объяснения), но интересно знать, что существует более чем один полезный способ разделить действительные числа.
Действительные числа, включающие в себя все виды чисел, о которых мы говорили до сих пор, чрезвычайно важны при решении реальных математических задач во многих областях, особенно в науке и технике.
Комплексные числа
Когда вы умножаете два положительных числа друг на друга, вы получаете положительное число. Когда вы умножаете два отрицательных числа друг на друга, вы получаете положительное число. Итак, есть ли какое-нибудь число, которое можно умножить само на себя, чтобы получить отрицательное число? Да и нет. Такого действительного числа нет, но есть выдуманное число под названием i , которое при умножении само на себя становится отрицательным.Поскольку это не действительное число, мы называем его воображаемым числом (это своего рода небольшая математическая шутка).
Когда вы смешиваете действительные числа с мнимыми числами, например, складывая их вместе, вы получаете удивительный вид чисел, который называется комплексными числами . Почему они потрясающие? Во-первых, есть Фундаментальная теорема алгебры, которая верна для комплексных чисел так же, как Фундаментальная теорема арифметики верна для целых чисел. Основной раздел математики, называемый комплексным анализом, исследует свойства комплексных чисел.
Существуют ли в реальном мире мнимые или комплексные числа? На самом деле, в реальном мире чисел не существует. Мы используем числа для описания вещей, и да, в реальном мире есть вещи, которые мы описываем комплексными числами. Наверное, самый известный из них - электрические схемы; без использования комплексных чисел мы не смогли бы разработать современную электронику, которая лежит в основе многих современных технологий. Еще одна область, в которой важны комплексные числа, - это акустика, то есть научное изучение звука.
Еще виды номеров!
Есть много других видов чисел. Каждый из видов чисел интересен по-своему. Некоторые полезны для решения реальных проблем. Другие нет. Они могут иметь или не обладать свойствами, которые, как мы предполагаем, имеют «нормальные» числа. Например, мы обычно говорим, что «умножение коммутативно». Это означает, что вы можете изменить, какой фактор будет первым, не меняя результата, поэтому 2 x 3 равно 6, а 3 x 2 равно 6. Это верно для всех факторов, а не только для 2, 3 и 6.Однако, хотя умножение коммутативно, скажем, для действительных чисел, есть типы чисел, где это не так.
Придумывать и выяснять, как работают некоторые из этих чисел, - это весело. Абстрактная алгебра - это изучение того, какие фундаментальные свойства чисел приводят к каким другим важным свойствам. В этом исследовании есть много видов чисел, очень отличающихся от тех, к которым мы привыкли. Изучение некоторых из этих странных чисел похоже на изучение странных существ, обитающих на дне океана.Они могут быть действительно интересными!
Следующая тема: Сито Эратосфена
Об этом Bubbly Primes Math Help Page
404 | Микро Фокус
Сформируйте свою стратегию и преобразуйте гибридную ИТ-среду.
Помогите вам внедрить безопасность в цепочку создания стоимости ИТ и наладить сотрудничество между ИТ-операциями, приложениями и группами безопасности.
Помогите вам быстрее реагировать и получить конкурентное преимущество благодаря гибкости предприятия.
Ускорьте получение результатов гибридного облака с помощью услуг по консультированию, трансформации и внедрению.
Службы управления приложениями, которые позволяют поручить управление решениями экспертам, разбирающимся в вашей среде.
Услуги стратегического консалтинга для разработки вашей программы цифровой трансформации.
Полнофункциональное моделирование сценариев использования с предварительно созданными интеграциями в портфеле программного обеспечения Micro Focus, демонстрирующее реальный сценарий использования
Услуги экспертной аналитики безопасности, которые помогут вам быстро спроектировать, развернуть и проверить реализацию технологии безопасности Micro Focus.
Служба интеграции и управления услугами, которая оптимизирует доставку, гарантии и управление в условиях нескольких поставщиков.
Анализируйте большие данные с помощью аналитики в реальном времени и ищите неструктурированные данные.
Анализируйте большие данные с помощью аналитики в реальном времени и ищите неструктурированные данные.
Анализируйте большие данные с помощью аналитики в реальном времени и ищите неструктурированные данные.
Мобильные услуги, которые обеспечивают производительность и ускоряют вывод на рынок без ущерба для качества.
Анализируйте большие данные с помощью аналитики в реальном времени и ищите неструктурированные данные.
