Что такое реинтеграция википедия – Интеграция — что это такое простыми словами и как можно что-то интегрировать | Создание сайтов и заработок в сети — adijuhpalace.ru

Содержание

Реинтеграция (экономическая) — это… Что такое Реинтеграция (экономическая)?

Реинтеграция (экономическая): Повторное включение мигранта в экономическую систему его/ее страны происхождения. Мигрант получает возможность зарабатывать себе на жизнь. С точки зрения развития экономическая реинтеграция также направлена на использование опыта, приобретенного в другой стране, для содействия экономическому и социальному развитию страны происхождения.

Реинтеграция (социальная)
Реинтеграция

Смотреть что такое «Реинтеграция (экономическая)» в других словарях:

Исключительная экономическая зона — Морские зоны в соответствии с Конвенцией ООН по морскому праву. Исключительная экономическая зона … Википедия

Конфедеративные Штаты Америки — Confederate States of America Непризнанная конфедерация [1] … Википедия
Организация Объединённых Наций — Запрос «ООН» перенаправляется сюда; см. также другие значения. Запрос «UN» перенаправляется сюда; см. также другие значения. Координаты: 40°45′00″ с. ш. 73°58′03″ з. д … Википедия
БРИКС — Страны BRICS: Бразилия, Россия, Индия, Китай и ЮАР … Википедия
Шанхайская организация сотрудничества — (ШОС) 上海合作组织 … Википедия
Организация Договора о коллективной безопасности — ОДКБ Эмблема ОДКБ … Википедия
Суверенитет — (Sovereignty) Суверенитет это независимость государства от других стран Суверенитет России и его проблемы, суверенитет Украины, суверенитет республики Беларусь, суверенитет Казахстана, суверенитет Чечни, Проблемы суверенитета стран Европы,… … Энциклопедия инвестора
Организация Североатлантического договора — Проверить нейтральность. На странице обсуждения должны быть подробности. У этого термина существуют и другие значения, см. NATO (значения) … Википедия
Евразийское экономическое сообщество — Интеграция в Евразии … Википедия
Организация стран — Флаг ОПЕК … Википедия

Интеграция данных — Википедия

Интеграция данных включает объединение данных, находящихся в различных источниках, и предоставление данных пользователям в унифицированном виде. Этот процесс становится существенным как в коммерческих задачах (когда двум похожим компаниям необходимо объединить их базы данных), так и в научных (комбинирование результатов исследования из различных биоинформационных репозиториев, для примера). Роль интеграции данных возрастает, когда увеличивается объём и необходимость совместного использования данных. Это стало фокусом обширной теоретической работы, а многочисленные проблемы остаются нерешёнными

[прояснить].

Системы интеграции данных могут обеспечивать интеграцию данных на физическом, логическом и семантическом уровне. Интеграция данных на физическом уровне с теоретической точки зрения является наиболее простой задачей и сводится к конверсии данных из различных источников в требуемый единый формат их физического представления. Интеграция данных на логическом уровне предусматривает возможность доступа к данным, содержащимся в различных источниках, в терминах единой глобальной схемы, которая описывает их совместное представление с учетом структурных и, возможно, поведенческих (при использовании объектных моделей) свойств данных. Семантические свойства данных при этом не учитываются. Поддержку единого представления данных с учетом их семантических свойств в контексте единой онтологии предметной области обеспечивает интеграция данных на семантическом уровне.

[1]

Процессу интеграции препятствует неоднородность источников данных, в соответствии с уровнем интеграции. Так, при интеграции на физическом уровне в источниках данных могут использоваться различные форматы файлов. На логическом уровне интеграции может иметь место неоднородность используемых моделей данных для различных источников или различаются схемы данных, хотя используется одна и та же модель данных. Одни источники могут быть веб-сайтами, а другие — объектными базами данных и т. д. При интеграции на семантическом уровне различным источникам данных могут соответствовать различные онтологии. Например, возможен случай, когда каждый из источников представляет информационные ресурсы, моделирующие некоторый фрагмент предметной области, которому соответствует своя понятийная система, и эти фрагменты пересекаются.

При создании системы интеграции возникает ряд задач, состав которых зависит от требований к ней и используемого подхода. К ним, в частности, относятся:

Разработка архитектуры системы интеграции данных.
Создание интегрирующей модели данных, являющейся основой единого пользовательского интерфейса в системе интеграции.
Разработка методов отображения моделей данных и построение отображений в интегрирующую модель для конкретных моделей, поддерживаемых отдельными источниками данных.
Интеграция метаданных, используемых в системе источников данных.
Преодоление неоднородности источников данных.
Разработка механизмов семантической интеграции источников данных.

Консолидация[править | править код]

В случае консолидации данные извлекаются из источников, и помещаются в Хранилище данных. Процесс заполнения Хранилища состоит из трех фаз — извлечение, преобразование, загрузка (Extract, Transformation, Loading — ETL). Во многих случаях именно ETL понимают под термином «интеграция данных». Еще одна распространенная технология консолидации данных — управление содержанием корпорации (enterprise content management, сокр. ECM). Большинство решений ECM направлены на консолидацию и управление неструктурированными данными, такими как документы, отчеты и web-страницы.

Консолидация — однонаправленный процесс, то есть данные из нескольких источников сливаются в Хранилище, но не распространяются из него обратно в распределенную систему. Часто консолидированные данные служат основой для приложений бизнес-аналитики (Business Intelligence, BI), OLAP-приложений.

При использовании этого метода обычно существует некоторая задержка между моментом обновления информации в первичных системах и временем, когда данные изменения появляются в конечном месте хранения. Конечные места хранения данных, содержащие данные с большими временами отставания (например, более одного дня), создаются с помощью пакетных приложений интеграции данных, которые извлекают данные из первичных систем с определенными, заранее заданными интервалами. Конечные места хранения данных с небольшим отставанием обновляются с помощью оперативных приложений интеграции данных, которые постоянно отслеживают и передают изменения данных из первичных систем в конечные места хранения.

Федерализация[править | править код]

В федеративных БД физического перемещения данных не происходит: данные остаются у владельцев, доступ к ним осуществляется при необходимости (при выполнении запроса). Изначально федеративные БД предполагали создание в каждом из n узлов n-1 фрагментов кода, позволяющего обращаться к любому другому узлу. При этом федеративные БД отделяли от медиаторов^[2].

При использовании медиатора создается общее представление (модель) данных. Медиатор — посредник, поддерживающий единый пользовательский интерфейс на основе глобального представления данных, содержащихся в источниках, а также поддержку отображения между глобальным и локальным представлениями данных. Пользовательский запрос, сформулированный в терминах единого интерфейса, декомпозируется на множество подзапросов, адресованных к нужным локальным источникам данных. На основе результатов их обработки синтезируется полный ответ на запрос. Используются две разновидности архитектуры с посредником — Global as View и Local as View.

[1]

Отображение данных из источника в общую модель выполняется при каждом запросе специальной оболочкой (wrapper). Для этого необходима интерпретация запроса к отдельным источникам и последующее отображение полученных данных в единую модель. Сейчас этот способ также относят к федеративным БД.^[3]

Интеграция корпоративной информации (Enterprise information integration, сокр. EII) — это пример технологии, которая поддерживает федеративный подход к интеграции данных.

Изучение и профилирование первичных данных, необходимые для федерализации, несильно отличаются от аналогичных процедур, требуемых для консолидации.

Распространение данных[править | править код]

Приложения распространения данных осуществляют копирование данных из одного места в другое. Эти приложения обычно работают в оперативном режиме и производят перемещение данных к местам назначения, то есть зависят от определенных событий. Обновления в первичной системе могут передаваться в конечную систему синхронно или асинхронно. Синхронная передача требует, чтобы обновления в обеих системах происходили во время одной и той же физической транзакции. Независимо от используемого типа синхронизации, метод распространения гарантирует доставку данных в систему назначения. Такая гарантия — это ключевой отличительный признак распространения данных. Большинство технологий синхронного распространения данных поддерживают двусторонний обмен данными между первичными и конечными системами. Примерами технологий, поддерживающих распространение данных, являются интеграция корпоративных приложений (Enterprise application integration, сокр. EAI) и тиражирование корпоративных данных (Еnterprise data replication, сокр. EDR). От федеративных БД этот способ отличает двустороннее распространение данных.

[1]

Сервисный подход[править | править код]

Сервисно-ориентированная архитектура SOA (Service Oriented Architecture), успешно применяемая при интеграции приложений, применима и при интеграции данных. Данные также остаются у владельцев и даже местонахождение данных неизвестно. При запросе происходит обращение к определённым сервисам, которые связаны с источниками, где находится информация и её конкретный адрес.

Интеграция данных объединяет информацию из нескольких источников таким образом, чтобы её можно было показать клиенту в виде сервиса. Сервис — это не запрос в традиционном смысле обращения к данным, скорее, это извлечение некоторой бизнес-сущности (или сущностей), которое может быть выполнено сервисом интеграции через серию запросов и других сервисов. Подход SOA концентрируется, в первую очередь, на определении и совместном использовании в форме сервисов относительно ограниченного количества самых важных бизнес-функций в корпорации. Следовательно, сервис-ориентированные интерфейсы в довольно большой степени строятся на ограниченном количестве запросов на необходимую информацию, которую нужно представить потребителю.

Имея соответствующие учетные данные системы безопасности, потребитель может осуществить выборку любых данных из источника через почти неограниченное количество различных запросов SQL. Но для этого потребитель должен иметь представление о модели источника данных и способе создания результата с использованием этой базовой модели. Чем сложнее модель источника данных, тем более сложной может оказаться эта задача.^[4]

Кроме того[править | править код]

В ^[1] описан пример гибридного подхода.

Другая классификация методов приведена в ^[5].

Вне зависимости от выбранных технологии и метода интеграции данных, остаются вопросы, связанные с их смысловой интерпретацией и различиями в представлении одних и тех же вещей. Именно, приходится разрешать несоответствие схем данных ^[6] и несоответствие самих данных.

Типы несоответствия схем данных[править | править код]

Конфликты неоднородности (используются различные модели данных для различных источников)
Конфликты именования (в различных схемах используется различная терминология, что приводит к омонимии и синонимии в именовании)
Семантические конфликты (выбраны различные уровни абстракции для моделирования подобных сущностей реального мира)
Структурные конфликты (одни и те же сущности представляются в разных источниках разными структурами данных).

Структурные и семантические конфликты выливаются в следующие проблемы:

Различие в типах данных. Некоторый домен в одном источнике может представляться числом, в другом — строкой фиксированной длины, в третьем — строкой переменной длины.
Различие в единицах измерения. В одной БД указана величина в сантиметрах, в другой — в дюймах. В этом случае существует отображение 1:1.
Различие в множестве допустимых значений. Один и тот же признак может определяться разными наборами констант. Например, выполнение задания одним источником может оцениваться по четырехбальной шкале(неудовлетворительно, удовлетворительно, хорошо, отлично), другим — по трехбальной (-,±,+), третьим — по стобальной. Отображение не является 1:1, оно может быть многозначным, может не иметь обратного, может зависеть от сторонних данных (например, 30 по математике соответствовать «удовлетворительно», а по русскому языку — «неудовлетворительно»).
Различие «домен-отношение». Домен в одной БД (напр строковое значение) соответствует таблице в другой БД (записи из таблицы-справочника).
Различие «домен — группа доменов». В одном источнике адрес записывается одной строкой, в другом — отдельные поля для улицы, дома, строения, квартиры.
Различие «данные-схема». Данные одной БД соответствуют схеме (метаданным) другой. В одной БД «инженер» — значение атрибута «должность» отношения «работник», в другой «инженеры» — отношение, содержащее некоторых работников, в то время как «бухгалтеры» содержит других.
Отсутствующие значения. В каком-то из источников может отсутствовать информация, имеющаяся в большинстве других.

Разрешение этих несоответствий часто выполняется вручную. Обзор автоматических методов разрешения несоответствия схем можно найти в ^[7].

Типы несоответствия собственно данных[править | править код]

Различие формата данных. «ул. Бахрушина, 18-1» или «Бахрушина, д.18, стр.1»; «8(910)234-45-32» или «8-910-234-45-32»
Различие в представлении значений. Например, некая организация может быть записана в отдельных источниках как «Новолипецкий металлургический комбинат», «НЛМК», «ОАО НЛМК».
Потеря актуальности данных одним из источников. Например, смена фамилии при замужестве: в одной БД записана новая фамилия, в другой старая, и они не совпадают.
Наличие ошибок операторского ввода (или ошибок распознавания бланков) в отдельных источниках данных. Сюда относятся механические опечатки, ошибки восприятия на слух сложнопроизносимых имен/названий, отсутствие единых стандартов транскрипции с иностранных языков.
Намеренное внесение искажений с целью затруднить идентификацию сущностей.

Перечисленные различия приводят к дублированию записей при интеграции данных в одну БД. Разрешение перечисленных проблем и устранение дублирования записей вручную практически невозможно. Имеется множество методов для её автоматического и полуавтоматического решения. По-русски задача не имеет устоявшегося термина (применяются «сопоставление записей», «вероятностное соединение», «нестрогое соединение», «нестрогое соответствие»). В зарубежных работах эта задача носит название Identity resolution, или Record linkage (есть и другие синонимы). Обзор методов можно найти в ^[8].

↑ ¹ ² ³ ⁴ Когаловский М.Р. Методы интеграции данных в информационных системах (неопр.) (недоступная ссылка). Архивировано 22 июля 2012 года.
↑ Гарсиа-Молина Г., Ульман Дж., Уидом Дж. Системы баз данных. Полный курс = Database Systems: The Complete Book. — Вильямс, 2003. — 1088 с. — ISBN 5-8459-0384-X.
↑ Интеграция данных и Хранилища (неопр.).
↑ Гюнтер Зауфер, Мэй Сельваж, Эойн Лейн, Билл Мэтьюс. Шаблоны для информационного сервиса (неопр.) (03.08.2007). Архивировано 22 июля 2012 года.
↑ Леонид Черняк. Интеграция данных: синтаксис и семантика (неопр.). «Открытые системы» , № 10, 2009. Архивировано 22 июля 2012 года.
↑ William Kent. Solving Domain Mismatch and Schema Mismatch Problems with an Object-Oriented Database Programming Language (неопр.). Proceedings of the International Conference on Very Large Data Bases (1991). Архивировано 22 июля 2012 года.
↑ Erhard Rahm, Philip A. Bernstein. A Survey of Approaches to Automatic Schema Matching (неопр.). VLDB JOURNAL (2001). Архивировано 22 июля 2012 года.
↑ Ahmed K. Elmagarmid, Panagiotis G. Ipeirotis, Vassilios S. Verykios. Duplicate Record Detection: A Survey (неопр.). IEEE TRANSACTIONS ON KNOWLEDGE AND DATA ENGINEERING, VOL. 19, NO. 1, JANUARY 2007. Архивировано 22 июля 2012 года.

Реинтеграция (социальная) — это… Что такое Реинтеграция (социальная)?

Реинтеграция (социальная): Повторное включение мигранта в социальные структуры страны своего происхождения. Это, с одной стороны, создание круга общения (друзья, родственники, соседи), с другой – участие в структурах гражданского общества (объединениях, группах взаимопомощи и пр.)

Реинтеграция (культурная)
Реинтеграция (экономическая)

Смотреть что такое «Реинтеграция (социальная)» в других словарях:

ГОСТ Р 52495-2005: Социальное обслуживание населения. Термины и определения — Терминология ГОСТ Р 52495 2005: Социальное обслуживание населения. Термины и определения оригинал документа: 2.1.6 адресность: Принцип социального обслуживания населения, предусматривающий предоставление социальных услуг конкретным лицам… … Словарь-справочник терминов нормативно-технической документации
Конфедеративные Штаты Америки — Confederate States of America Непризнанная конфедерация [1] … Википедия
Суверенитет — (Sovereignty) Суверенитет это независимость государства от других стран Суверенитет России и его проблемы, суверенитет Украины, суверенитет республики Беларусь, суверенитет Казахстана, суверенитет Чечни, Проблемы суверенитета стран Европы,… … Энциклопедия инвестора
Организация Объединённых Наций — Запрос «ООН» перенаправляется сюда; см. также другие значения. Запрос «UN» перенаправляется сюда; см. также другие значения. Координаты: 40°45′00″ с. ш. 73°58′03″ з. д … Википедия
Международное право охраны окружающей среды — (международное право окружающей среды, международное экологическое право, интерэкоправо) – это совокупность норм и принципов, регулирующих международные отношения в сфере защиты окружающей среды в целях охраны и рационального использования… … Википедия
ФЕНОМЕНОЛОГИЯ — (от греч. phainomenon являющееся) одно из главных направлений в философии 20 в. Основатель этого направления Э. Гуссерль, непосредственные предшественники Ф. Брентано и К. Штумпф. Исходный пункт Ф. кн. Гуссерля «Логические исследования» (т. 1 2,… … Философская энциклопедия
Нюрнбергский процесс — У этого термина существуют и другие значения, см. Нюрнбергский процесс (значения) … Википедия
Женевские конвенции — Оригинальный документ. Женевские конвенции ряд международных соглашений, заключенных на конференциях в Женеве (Швейцария). Жен … Википедия
Колония — В Викисловаре есть статья «колония» См. также: Римская колония У этого термина существуют и друг … Википедия
Совет Европы — Не следует путать с Европейским советом органом Европейского союза. Совет Европы Council of Europe Conseil de l Europe Флаг Совет … Википедия

Интеграл — Википедия

Интеграл — одно из важнейших понятий математического анализа, которое возникает при решении задач о нахождении площади под кривой, пройденного пути при неравномерном движении, массы неоднородного тела, и тому подобных, а также в задаче о восстановлении функции по её производной (неопределённый интеграл)^[1]. Упрощённо интеграл можно представить как аналог суммы для бесконечного числа бесконечно малых слагаемых. В зависимости от пространства, на котором задана подынтегральная функция, интеграл может быть — двойной, тройной, криволинейный, поверхностный и так далее; также существуют разные подходы к определению интеграла — различают интегралы Римана, Лебега, Стилтьеса и другие^[2].

Неопределённый интеграл[править | править код]

Пусть дана f(x){\displaystyle f(x)} — функция действительной переменной. Неопределённым интегралом функции f(x){\displaystyle f(x)}, или её первообразной, называется такая функция F(x){\displaystyle F(x)}, производная которой равна f(x){\displaystyle f(x)}, то есть F′(x)=f(x){\displaystyle F'(x)=f(x)}. Обозначается это так:

F(x)=∫f(x)dx{\displaystyle F(x)=\int f(x)dx}

В этой записи ∫{\displaystyle \int } — знак интеграла, f(x){\displaystyle f(x)} называется подынтегральной функцией, а dx{\displaystyle dx} — элементом интегрирования.

Первообразная существует не для любой функции. Легко показать, что по крайней мере все непрерывные функции имеют первообразную. Поскольку производные двух функций, отличающихся на константу, совпадают, в выражение для неопределённого интеграла включают произвольную постоянную C{\displaystyle C}, например

∫x2dx=x33+C,∫cos⁡(x)dx=sin⁡(x)+C{\displaystyle \int x^{2}dx={\frac {x^{3}}{3}}+C,\qquad \int \cos(x)dx=\sin(x)+C}

Операция нахождения интеграла называется интегрированием. Операции интегрирования и дифференцирования обратны друг другу в следующем смысле:

ddx∫f(x)dx=f(x),∫df(x)dxdx=f(x)+C{\displaystyle {\frac {d}{dx}}\int f(x)dx=f(x),\qquad \int {\frac {df(x)}{dx}}dx=f(x)+C}

Определённый интеграл[править | править код]

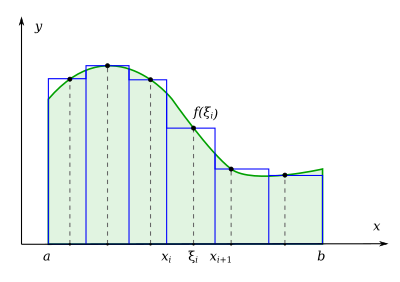${\frac {d}{dx}}\int f(x)dx=f(x),\qquad \int {\frac {df(x)}{dx}}dx=f(x)+C$

Интеграл как площадь криволинейной трапеции

Понятие определённого интеграла возникает в связи с задачей о нахождении площади криволинейной трапеции, нахождении пути по известной скорости при неравномерном движении и т. п.

Что такое интеграл, анимация (нажмите для воспроизведения)

Рассмотрим фигуру, ограниченную осью абсцисс, прямыми x=a{\displaystyle x=a} и x=b{\displaystyle x=b} и графиком функции y=f(x){\displaystyle y=f(x)}, называемую криволинейной трапецией (см. рисунок). Если по оси абсцисс отложено время, а по оси ординат — скорость тела, то площадь криволинейной трапеции есть пройденный телом путь.

Для вычисления площади этой фигуры естественно применить следующий приём. Разобьём отрезок [a;b]{\displaystyle [a;b]} на меньшие отрезки точками xi{\displaystyle x_{i}}, такими что a=x0<…<xi<xi+1<…<xn=b{\displaystyle a=x_{0}<…<x_{i}<x_{i+1}<…<x_{n}=b}, а саму трапецию — на ряд узких полосок, лежащих над отрезками [xi;xi+1]{\displaystyle [x_{i};x_{i+1}]}. Возьмём в каждом отрезке по произвольной точке ξi∈[xi;xi+1]{\displaystyle \xi _{i}\in [x_{i};x_{i+1}]}. Ввиду того, что длина i{\displaystyle i}-го отрезка Δxi=xi+1−xi{\displaystyle \Delta x_{i}=x_{i+1}-x_{i}} мала, будем считать значение функции f(x){\displaystyle f(x)} на нём примерно постоянным и равным yi=f(ξi){\displaystyle y_{i}=f(\xi _{i})}. Площадь криволинейной трапеции будет приблизительно равна площади ступенчатой фигуры, изображённой на рисунке:

S≈∑i=0n−1yiΔxi(∗){\displaystyle S\approx \sum _{i=0}^{n-1}y_{i}\Delta x_{i}\qquad (*)}

Если же теперь увеличивать число точек разбиения, так, чтобы длины всех отрезков неограниченно убывали (maxΔxi→0{\displaystyle \max \Delta x_{i}\to 0}), площадь ступенчатой фигуры будет всё ближе к площади криволинейной трапеции.

Поэтому мы приходим к такому определению:

Если существует, независимо от выбора точек разбиения отрезка и точек ξi{\displaystyle \xi _{i}}, предел суммы (*) при стремлении длин всех отрезков к нулю, то такой предел называется определённым интегралом (в смысле Римана) от функции f(x){\displaystyle f(x)} по отрезку [a;b]{\displaystyle [a;b]} и обозначается

∫abf(x)dx{\displaystyle \int \limits _{a}^{b}f(x)dx}

Сама функция при этом называется интегрируемой (в смысле Римана) на отрезке [a;b]{\displaystyle [a;b]}. Суммы вида (*) называются интегральными суммами.

Примеры интегрируемых функций:

Пример неинтегрируемой функции: функция Дирихле (1 при x{\displaystyle x} рациональном, 0 при иррациональном). Поскольку множество рациональных чисел всюду плотно в R{\displaystyle {\mathbb {R} }}, выбором точек ξi{\displaystyle \xi _{i}} можно получить любое значение интегральных сумм от 0 до b−a{\displaystyle b-a}.

Между определённым и неопределённым интегралом имеется простая связь. А именно, если

∫f(x)dx=F(x)+C{\displaystyle \int f(x)dx=F(x)+C}

то

∫abf(x)dx=F(b)−F(a){\displaystyle \int \limits _{a}^{b}f(x)dx=F(b)-F(a)}

Это равенство называется формулой Ньютона-Лейбница.

Интеграл в пространствах большей размерности[править | править код]

Двойные и кратные интегралы[править | править код]

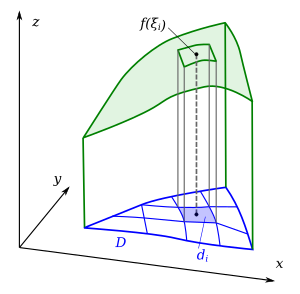$\int \limits _{a}^{b}f(x)dx=F(b)-F(a)$ Двойной интеграл как объём цилиндрического бруса

Понятие двойного интеграла возникает при вычислении объёма цилиндрического бруса, подобно тому, как определённый интеграл связан с вычислением площади криволинейной трапеции. Рассмотрим некоторую двумерную фигуру D{\displaystyle D} на плоскости XY{\displaystyle XY} и заданную на ней функцию двух переменных f(x,y){\displaystyle f(x,y)}. Понимая эту функцию как высоту в данной точке, поставим вопрос о нахождении объёма получившегося тела (см. рисунок). По аналогии с одномерным случаем, разобьём фигуру D{\displaystyle D} на достаточно малые области di{\displaystyle d_{i}}, возьмём в каждой по точке ξi=(xi,yi){\displaystyle \xi _{i}=(x_{i},y_{i})} и составим интегральную сумму

∑if(xi,yi)S(di){\displaystyle \sum _{i}f(x_{i},y_{i})S(d_{i})}

где S(di){\displaystyle S(d_{i})} — площадь области di{\displaystyle d_{i}}. Если существует, независимо от выбора разбиения и точек ξi{\displaystyle \xi _{i}}, предел этой суммы при стремлении диаметров областей к нулю, то такой предел называется двойным интегралом (в смысле Римана) от функции f(x,y){\displaystyle f(x,y)} по области D{\displaystyle D} и обозначается

∫Df(x,y)dS{\displaystyle \int \limits _{D}f(x,y)dS}, ∫Df(x,y)dxdy{\displaystyle \int \limits _{D}f(x,y)dxdy}, или ∬Df(x,y)dxdy{\displaystyle \iint \limits _{D}f(x,y)dxdy}

Объём цилиндрического бруса равен этому интегралу.

Криволинейный интеграл[править | править код]

Поверхностный интеграл[править | править код]

К понятию интеграла естественным образом приводит также задача о массе неоднородного тела. Так, масса тонкого стержня с переменной плотностью ρ(x){\displaystyle \rho (x)} даётся интегралом

M=∫ρ(x)dx{\displaystyle M=\int \rho (x)dx}

в аналогичном случае плоской фигуры

M=∬ρ(x,y)dxdy{\displaystyle M=\iint \rho (x,y)dxdy}

и для трёхмерного тела

M=∭ρ(x,y,z)dxdydz{\displaystyle M=\iiint \rho (x,y,z)dxdydz}

Интеграл Лебега[править | править код]

В основе определения интеграла Лебега лежит понятие σ{\displaystyle \sigma }-аддитивной меры. Мера является естественным обобщением понятий длины, площади и объёма.

Интеграл Лебега функции f{\displaystyle f} определённой на пространстве X{\displaystyle X} по мере μ{\displaystyle \mu } обозначают

∫Xfμ{\displaystyle \int \limits _{X}f\mu }, ∫x∈Xf(x)μ{\displaystyle \int \limits _{x\in X}f(x)\mu } или ∫Xf(x)μ(dx){\displaystyle \int \limits _{X}f(x)\mu (dx)}

последнее два обозначения употребляют если необходимо подчеркнуть что интегрирование ведётся по переменной x{\displaystyle x}. Однако часто пользуются следующим не вполне правильным обозначением

∫Xfdμ.{\displaystyle \int \limits _{X}fd\mu .}

Полагая меру отрезка (прямоугольника, параллелепипеда) равной его длине (площади, объёму), а меру конечного либо счётного объединения непересекающихся отрезков (прямоугольников, параллелепипедов), соответственно, сумме их мер, и продолжая эту меру на более широкий класс измеримых множеств, получим т. наз. Лебегову меру на прямой (в R2{\displaystyle {\mathbb {R} }^{2}}, в R3){\displaystyle {\mathbb {R} }^{3})}.

Естественно, в этих пространствах возможно ввести и другие меры, отличные от Лебеговой. Меру можно ввести также на любом абстрактном множестве. В отличие от интеграла Римана, определение интеграла Лебега остаётся одинаковым для всех случаев. Идея его состоит в том, что при построении интегральной суммы значения аргумента группируются не по близости к друг другу (как в определении по Риману), а по близости соответствующих им значений функции.

Пусть есть некоторое множество X{\displaystyle X}, на котором задана σ{\displaystyle \sigma }-аддитивная мера μ{\displaystyle \mu }, и функция f:X→R{\displaystyle f:X\to {\mathbb {R} }}. При построении интеграла Лебега рассматриваются только измеримые функции, то есть такие, для которых множества

Ea={x∈X:f(x)<a}{\displaystyle E_{a}=\{x\in X:f(x)<a\}}

измеримы для любого a∈R{\displaystyle a\in {\mathbb {R} }} (это эквивалентно измеримости прообраза любого борелевского множества).

Сначала интеграл определяется для ступенчатых функций, то есть таких, которые принимают конечное или счётное число значений ai{\displaystyle a_{i}}:

∫Xfμ=∑iaiμ(f−1(ai)){\displaystyle \int \limits _{X}f\mu =\sum _{i}a_{i}\mu (f^{-1}(a_{i}))}

где f−1(ai){\displaystyle f^{-1}(a_{i})} — полный прообраз точки ai{\displaystyle a_{i}}; эти множества измеримы в силу измеримости функции. Если этот ряд абсолютно сходится, ступенчатую функцию f{\displaystyle f} назовём интегрируемой в смысле Лебега. Далее, назовём произвольную функцию f{\displaystyle f} интегрируемой в смысле Лебега, если существует последовательность интегрируемых ступенчатых функций fn{\displaystyle f_{n}}, равномерно сходящаяся к f{\displaystyle f}. При этом последовательность их интегралов также сходится; её предел и будем называть интегралом Лебега от функции f{\displaystyle f} по мере μ{\displaystyle \mu }:

∫Xfμ=lim∫Xfnμ{\displaystyle \int \limits _{X}f\mu =\lim \int \limits _{X}f_{n}\mu }

Если рассматривать функции на Rn{\displaystyle {\mathbb {R} }^{n}} и интеграл по мере Лебега, то все функции, интегрируемые в смысле Римана, будут интегрируемы и в смысле Лебега. Обратное же неверно (например, функция Дирихле не интегрируема по Риману, но интегрируема по Лебегу, так как равна нулю почти всюду). Фактически, любая ограниченная измеримая функция интегрируема по Лебегу.

Основные понятия интегрального исчисления введены в работах Ньютона и Лейбница в конце XVII века (первые публикации состоялись в 1675 году). Лейбницу принадлежит обозначение интеграла ∫ydx{\displaystyle \int ydx}, напоминающее об интегральной сумме, как и сам символ ∫{\displaystyle \int }, от буквы ſ («длинная s») — первой буквы в латинском слове summa (тогда ſumma, сумма)^[3]. Сам термин «интеграл» предложен Иоганном Бернулли, учеником Лейбница. Обозначение пределов интегрирования в виде ∫ab{\displaystyle \int _{a}^{b}} введено Фурье в 1820 году.

Строгое определение интеграла для случая непрерывных функций сформулировано Коши в 1823 году, а для произвольных функций — Риманом в 1853 году. Определение интеграла в смысле Лебега впервые дано Лебегом в 1902 году (для случая функции одной переменной и меры Лебега).

Виноградов И. М. (гл. ред.). Интеграл // Математическая энциклопедия. — М., 1977. — Т. 2.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: Наука, 1969.
Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — М.: Наука, 1976.

социальная реинтеграция — это… Что такое социальная реинтеграция?

социальная реинтеграция: Sociology: social reintegration

социальная революция
социальная реинтеграция наркоманов

Смотреть что такое «социальная реинтеграция» в других словарях:

Реинтеграция (социальная) — Повторное включение мигранта в социальные структуры страны своего происхождения. Это, с одной стороны, создание круга общения (друзья, родственники, соседи), с другой – участие в структурах гражданского общества (объединениях, группах… … Международное миграционное право: глоссарий терминов
ГОСТ Р 52495-2005: Социальное обслуживание населения. Термины и определения — Терминология ГОСТ Р 52495 2005: Социальное обслуживание населения. Термины и определения оригинал документа: 2.1.6 адресность: Принцип социального обслуживания населения, предусматривающий предоставление социальных услуг конкретным лицам… … Словарь-справочник терминов нормативно-технической документации
Конфедеративные Штаты Америки — Confederate States of America Непризнанная конфедерация [1] … Википедия
Суверенитет — (Sovereignty) Суверенитет это независимость государства от других стран Суверенитет России и его проблемы, суверенитет Украины, суверенитет республики Беларусь, суверенитет Казахстана, суверенитет Чечни, Проблемы суверенитета стран Европы,… … Энциклопедия инвестора
Организация Объединённых Наций — Запрос «ООН» перенаправляется сюда; см. также другие значения. Запрос «UN» перенаправляется сюда; см. также другие значения. Координаты: 40°45′00″ с. ш. 73°58′03″ з. д … Википедия
Международное право охраны окружающей среды — (международное право окружающей среды, международное экологическое право, интерэкоправо) – это совокупность норм и принципов, регулирующих международные отношения в сфере защиты окружающей среды в целях охраны и рационального использования… … Википедия
ФЕНОМЕНОЛОГИЯ — (от греч. phainomenon являющееся) одно из главных направлений в философии 20 в. Основатель этого направления Э. Гуссерль, непосредственные предшественники Ф. Брентано и К. Штумпф. Исходный пункт Ф. кн. Гуссерля «Логические исследования» (т. 1 2,… … Философская энциклопедия
Нюрнбергский процесс — У этого термина существуют и другие значения, см. Нюрнбергский процесс (значения) … Википедия
Женевские конвенции — Оригинальный документ. Женевские конвенции ряд международных соглашений, заключенных на конференциях в Женеве (Швейцария). Жен … Википедия
Колония — В Викисловаре есть статья «колония» См. также: Римская колония У этого термина существуют и друг … Википедия
Совет Европы — Не следует путать с Европейским советом органом Европейского союза. Совет Европы Council of Europe Conseil de l Europe Флаг Совет … Википедия

Красивое описание стамбула: Стамбул, Турция: фото и описание города, достопримечательности – Турция, Стамбул — описание, транспорт, интересные места, пляжи, магазины, меры предосторожности.

Когда лучше ехать на море в грецию – 11 мест, куда лучше поехать – 2020 Отзывы туристов и форум «Ездили-Знаем!» * Греция

Что такое реинтеграция википедия – Интеграция — что это такое простыми словами и как можно что-то интегрировать | Создание сайтов и заработок в сети